Algoritmi
Probleme propuse
1. a si b retini valorile pentru doua numere intregi citite de la tastatura. Sa se interschimbe valorile celor doua numere.
2. cunoscand cele 5 note obtinute de un elev la informatica pe parcursul unui semestru si nota de la teza scrieti unalgoritm care sa afiseze media lui.
3. Fie un numar format din trei cifre. Sa se afiseze cifrele sale incepand cu cifra unitatilor.
4.
Se citeste un numar natural format
din 4 cifre. Afisati numerele obtinute in urmatoarele moduri:
–schimband prima cifra cu ultima
-schimband intre ele cifrele din mijloc
5. Fie a un numar natural format din 5 cifre. Scrieti un algoritm care sa deterine si sa afiseze numarul format din prima, a treia si a cincea cifra din a.
6. Scrieti un algoritm care sa determine cel mai mare dintre doua numere intregi citite.
7. Scrieti un algorim care sa determine cel mai mare dintre 3 numere intregi citite.
8. Scrieti un program care citeste de la tastatura trei valori numerice a, b, c si apoi afiseaza pe ecran cea mai mare diferenta dintre oricare doua valori date.
9. Ex. a=100, b=15, c=105. Se va afisa 90.
10. Se da un numar din 3 cifre.Sa se genereze cel mai mare numar care are aceleasi cifre ca el.
11. Intr-un parc se joaca 3 copii care au greutatile a,b,c. Sa se stabileasca daca se pot aseza pe un balansoar astfel incat acesta sa stea in echilibru.
12. Sa se rezolve ecuatia de gradul I cu o necunoscuta: ax+b=0 unde a si b sunt coeficienti reali cititi. Discutie.
13. Sa se rezolve ecuatia de gradul al II-lea cu 2 necunoscute: ax2+bx+c=0 unde a,b,c sunt coeficienti reali cititi. Discutie.
14. Se citesc de la tastatura coordonatele x si y ale celor trei varfuri ale unui triungi. Sa se scrie un algoritm care citeste aceste valori si verifica daca acestea pot constitui varfurile triunghiului. In caz afirmativ se va afisa tipul triunghiului (oarecare, isoscel sau echilateral).
15. Sa se determine cel mai mare divizor comun a doua numere naturale a si b citite.
16. Sa se determine suma cifrelor unui numar natural
17. Sa se determine cate cifre are un numar natural
18. Sa se determine cifra cea mai mare a unui numar natural
19. Se citeste un numar atural de maxim 9 cifre. Sa se determine de cate ori se gaseste cifra 7 in scrierea lui
20. Un bancher are un seif cu cifru. Pentru a nu uita cifrul, vrea sa-l
scrie pe o foaie, dar codificat: fiecare cifra sa fie inlocuita cu diferenta
dintre cifra 9 si cifra respectiva. Codificati numarul bancherului.De exemplu
pentru 386281 veti obtine 613178.
STRUCTURI REPETITIVE
21. Suma, produsul, media aritmetică a primelor n numere naturale.
22. Inversarea unui număr. Verificarea dacă un număr este palindrom.
23. Suma cifrelor unui număr.
24. Verificarea dacă un număr este prim.
25. Să se afişeze şi să se contorizeze toate numerele prime din intervalul [a,b].
26. Determinarea divizorilor unui număr. Suma divizorilor.
27. Să se determine numerele perfecte până la n (egale cu suma divizorilor lor).
28. Ridicarea la o putere întreagă a unui număr.
29. Să se calculeze suma S=1k+2k+3k+………+nk.
30. Descompunerea unui număr în factori ireductibili.
31. Algoritmul lui Euclid. Determinarea cmmdc şi cmmmc a 2 numere.
32. Suma a două fracţii cu afişarea rezultatului sub formă de fracţie ireductibilă.
33. Conjectura lui Goldbach: orice număr par mai mare decât 4 se poate scrie ca sumă de două numere prime. Să se descompună un număr par ł4 ca sumă de două nr. prime.
34. 
Să se determine perechile de numere gemene până la n citit (numere prime impare
consecutive).
35. Să se determine un număr până la n citit care să aibă un număr maxim de divizori.
36. Se citeşte un număr cu n cifre (nŁ9). Să se determine numărul obţinut prin eliminarea cifrei / cifrelor din mijloc.
37. Cifra de control a unui număr.
38. Să se afişeze numerele de la 1 la n care sunt egale cu suma factorialelor cifrelor sale. (Ex: 145=1!+4!+5!)
39. Să se genereze toate cuburile perfecte până la n citit.
40. Să se afişeze toate numerele până la n care sunt egale cu suma cuburilor cifrelor sale.
41. Să se genereze toate numerele pitagorice până la n citit.
TABLOURI
UNIDIMENSIONALE
42.
Să se ordoneze crescător
/ descrescător un vector.
43.
Sa se afiseze
acele elemente dintr-un vector care sunt prime.
44. Determinarea maximului / minimului unui vector şi afişarea poziţiilor pe care apar.
45. Să se rotească un vector cu o poziţie la dreapta / stânga (ultimul element devine primul, respectiv primul element devine ultimul).
46. Rotirea unui vector cu k poziţii la stânga (dreapta).
47.
Să se mute
la sfârşitul unui tablou toate elementele nule.
48. Să se incarce într-un vector toate numerele prime până la n care, inversate, sunt tot prime.
49.
Sa se ordoneze
un vector astfel incat elementele de pe pozitiile impare vor fi ordonate crescator iar cele de
pe pozitiile pare sa fie ordonate descrecator.
50. Suma şi produsul a două polinoame.
51. Valoarea unui polinom într-un punct.
52.
Să se verifice dacă un vector este ordonat
(crescător sau descrescător).
53. 
Dându-se un vector neordonat cu n
componente diferite, să se determine elementul cu numărul de ordine k din tabloul ordonat crescător,
fără a se ordona tabloul.
54. 
Dându-se un vector neordonat cu n
componente diferite, să se determine poziţia elementului a[k] în tabloul ordonat crescător, fără a se ordona tabloul.
55. Să se găsească un element k printre elementele unui vector. Dacă se găseşte, să se afişeze poziţiile pe care apare. Dacă nu, să se dea un mesaj.
56. Interclasarea a doi vectori (ordonaţi sau nu).
57. Fie doi vectori x şi y, de mărime n. Să se calculeze:
a) E=(x1+y1)* (x2+y2)* ......*(xn+yn)
b) E=x1y1+ x2y2 +......+xnyn
c) E=min(x1,y1)+min(x2,y2)+ ......min(xn,yn)
d) E=min(x1,yn)+min(x2,yn-1)+ ......min(xn,y1)
58. Să se numere de câte ori se întâmplă ca într-un vector, un element să fie egal cu suma (produsul, media aritmetică, geometrică) vecinilor săi.
59. Să se determine media aritmetică a elementelor unui vector, în care elementele egale se vor lua o singură dată.
60. Să se verifice dacă elementele unui şir pot forma o progresie aritmetică (geometrică). Dacă da, să se afişeze raţia.
61. Să se inverseze un vector în el însuşi.
62. Să se afişeze şi să se numere elementele pare de pe poziţiile impare ale unui vector.
63. Se citeşte un vector cu n componente. Să se calculeze media aritmetică a elementelor pozitive din vector.
64. Să se insereze un element într-un vector, la poziţia k. Să se repete operaţia de mai multe ori.
65. Să se şteargă un elementul din poziţia k dintr-un vector.
66. Să se calculeze cmmdc a n numere naturale.
67. Se citeşte un vector cu n componente numere întregi. Să se construiască vectorul format din suma (produsul) cifrelor elementelor din primul vector.
68. Fie doi vectori a şi b cu m, respectiv n elemente numere reale. Să se afişeze câte din componentele vectorului a sunt strict mai mici decât toate componentele vectorului b.
69. Să se afişeze primele n elemente din şirul lui Fibonacci.
70. Să se decidă dacă elementele unui vector sunt distincte.
71. Să se afişeze diferenţa, intersecţia, reuniunea şi produsul cartezian a două mulţimi de numere reale.
72. Sa se genereze un vector care sa retina toate numerele forate din 3 cifre distincte divizibile cu 4.
73. Sa se determine daca un vector este palindromic
74. Sa se determine cea mai lunga secventa palindromica dintr-un vector
75. Sa se incarce intr-un vector primele n numere prime
76. Fie v un vector de intregi. Sa se genereze doi vectori: unul care contine elementele pozitive si altul care contine elementele negative
77. Operatii cu multimi: intersectia, diferenta, reuniunea.
78. Sa se determine cea mai mare suma obtinuta dintr-un sir de numere intregi.
79. Sa se elimine elementele care se repete dintr-un vector.
80. Operatii cu fractii: suma, produsul a n fractii.
81. Sa se determine cea mai mare (mica) fractie dintr-un sir de fractii
82. sa se simuleze extragerea unor bile numerotate de la 0 la n citit. Extragerea se intrerupe la 0. sa se determine suma extrasa. Nu se poate extrage aceeasi bila (numar) de doua ori.
83. Sa se determine daca intr-un vector de numere intregi exista o valoare care poate fi exprimata ca suma pozitiilor de inainte. In caz afirmativ se va afisa pozitia pe care se gaseste.
84. Sa se determine daca radical de ordinul m din (x1*x2*x2*….*xn) este numar natural.
TABLOURI
BIDIMENSIONALE
85. Suma şi produsul a două matrice.
86. Calcule pe zone ale unei matrice pătratice (zona de deasupra diagonalei principale sau secundare, de sub diagonale, cele 4 zone determinate de cele două diagonale).
87. Să se verifice dacă diagonalele unei matrice au elemente comune.
88. Să se calculeze cea mai mică dintre sumele pe linie sau pe coloană ale elementelor unei matrice m x n. Să se precizeze linia sau coloana pe care apare această sumă.
89. Determinarea maximului / minimului unei matrice.
90. Să se bordeze matricea Amxn cu linia m+1 şi coloana n+1, unde A[m+1,j] reprezintă suma elementelor de pe coloana j şi A[i,n+1] reprezintă suma elementelor de pe linia i.
91. Să se verifice dacă o matrice este rară (are mai mult de 2/3 zerouri).
92. Fie o matrice Amxn. Să se rearanjeze elementele matricei
astfel încât să fie în ordine crescătoare, citite de la stânga la
dreapta, linie cu linie.
Ex: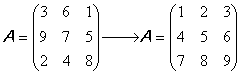 
93. 
Fiind dată o matrice Amxn, să se elimine toate
liniile care conţin zerouri.
94. 
Fiind dată o matrice Amxn, să se elimine toate liniile
şi coloanele care au la intersecţia lor zerouri.
95. Să se calculeze procentul elementelor pozitive (prime, pare, etc.) dintr-o matrice.
96. Să se calculeze şi să se afişeze produsul elementelor de pe coloanele pare (liniile impare) ale unei matrice.
97. Să se interschimbe liniile (coloanele) p şi q ale unei matrice.
98. Interschimbaţi coloanele unei matrice Amxn astfel încât
elementele de pe linia k să fie
ordonate crescător.
99. Să se verifice dacă o matrice pătratică este pătrat magic (suma elementelor de pe fiecare linie, coloană şi diagonală este aceeaşi).
Ex: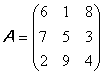 
100. 
Să se afişeze elementele unui tablou în ordinea
rezultată prin parcurgerea în spirală a tabloului, începând cu
elementul (1,1), în sensul acelor de ceas.
101. Rearanjaţi liniile unei matrice pătratice Anxn astfel încât elementele de pe diagonala principală să fie maxime pe linia pe care se află.
102. Sortarea prin inserţie a unui vector.
103. Sortarea unui vector prin selectarea minimului.
104. Sortarea unui vector prin numărare.
105. Sortarea unui vector astfel: prima jumătate crescător, a doua jumătate descrescător, folosind metode diferite.
106. 
Să se calculeze 2100.
Indicaţie: Păstraţi cifrele numărului obţinut prin fiecare înmulţire cu 2 într-un vector. Iniţial se porneşte de la vectorul (0,0....0,0,1).
107. Simulaţi înmulţirea unui număr cu mai mult de 3 cifre cu
un număr format dintr-o singură cifră.
108. Simulaţi înmulţirea unui număr cu oricât de multe cifre
cu un număr format din oricât de multe cifre.
109. Sa se determine daca o matrice are toate elementele egale
110. Sa se determine cate linii au valori reale
111. Sa se determine cel mai mare divizor comun al elementelor unei matrici
112. Fie o matrice cu m linii si n coloane avand componente binare: 0 sau 1.Fiecare dintre linii va reprezenta un numar binar. Sa se afiseze numerele corespunzatoare in baza 10
Ex pt m=5 si n=4 si:
0 0 1 1
1 0 0 1
1 1 1 0
0 1 0 1
0 0 0 0
113. Se considera un tablou bidimensional cu n linii si n coloane avand componente binare care codifica o harta ale carei tari sunt numerotate cu 1,2 ,…, n. Un element a[I,j]=1 daca tarile I si j sunt vecine. Sa se afiseze cati vecini are fiecare tara.
114. Sa se determine daca un tablou bidimensional, nxn , este simetric:
1 2 3 4 este simetric
2 7 5 6
3 5 2 1
4 6 1 3
115. sa se genereze elementele unei matrici patratice (nxn) astfel:
-elementele de pe diagonala secundara sa fie nule
-elementele de deasupra diagonalei secundare sa fie egale cu 1
-elementele situate sub diagonala secundara sa fie 2
ex pt n=4
1 1 1 0
1 1 0 2
1 0 2 2
0 2 2 2
116. sa se treaca un vector cu mxn elemente char intr-o matrice de mxn elemente char
ex: m=3 si n=2
v=(‘a’ ,’b’, ‘c’,’d’,’e’,’f’,’g’)
trece in
a b
c d
f g
117. Sa se afiseze elementele sa dintr-o matrice (minime pe linie si maxime pe coloana pe care se gasesc) si pozitia lor.
118. Sa se determine oglindita la dreapta (stanga, sus, jos ) a unei matrici
119. Sa se determine daca o matrice b este oglindita la dreapata a unei matrici a
120. Fie o matrice avand mxn componente intregi. Sa se afiseze acele elemente ale matricii (valoarea si coordonatele) pentru care suma elementelor pe linie este egala cu suma elementelor pe coloana.
121. La o clasa de elevi se pastreaza pe calculator mediile pe semestrul I ale fiecarui elev, la fiecare disciplina. Sa se scrie un program care citeste dintr-un fisier numarul elevilor, numarul disciplinelor si aploi afiseaza mediile elevilor.
122. Intr-o livada mare pomii sunt plantati pe randuri, formand o matrice. Pentru fiecare pom se cunoaste varsta lui. Proprietarul livezii vrea sa-si construiasca o casa, undeva la marginea livezii, dar nu are suficient spatiu. Se hotaraste sa taie cel mai batran pom de pe marginea livezii. Scrieti un program care sa rezolve aceasta problema , afisand un mesaj corespunzator.
123. Pe o tabla de sah de dimensiune n*n sunt asezate n dame. Sa se determine cate dame de pe tabla nu sunt atacate.
124. Un teren muntos are forma de matrice de m*n zone. Pentru fiecare zona se retine altitudinea. Sa se determine zonele varf (inconjurate de altitudini mai mici).
125. Fie o matrice care retine cifre de la 0 la 9. Sa se afiseze suma numerelor care se pot forma din cifrele fiecarei linii.
Exemplu:
0 6 8 2 4
9 7 0 5 8
3 1 7 9 5
se va calcula 6824+97058+31795=135677
126. SE citeste o matrice mxn. Sa se roteasca matricea cu 90 grade in sens orar. Generalizare: sa se roteasca de x ori si sa se afiseze de ficare data.
127. Sa se treaca un sir de p numere nenule intr-o matrice avand n coloane.
128. Sa se afiseze zonele triunghiulare:
129. Sa se elimine o linie/ coloana dintr-o matrice
130. Fie o matrice de intregi. Sa se determine numarul predominant din matrice (in procente)
131. Sa se interschimbe diagonala principala cu diagonala secundara a unei matrici patratice.
TIPUL MULŢIME (SET)
132. Operaţii cu mulţimi: apartenenţa unui element la o mulţime, reuniunea, intersecţia, diferenţa, diferenţa simetrică, produsul cartezian a două (n) mulţimi.
133. Să se verifice dacă elementele unui vector pot forma o mulţime.
134. Să se verifice dacă n mulţimi sunt sau nu disjuncte (oricare două nu au nici un element comun).
135. Să se calculeze cardinalul unei mulţimi (folosind o funcţie).
TIPUL STRING (ŞIR DE CARACTERE)
136. Să se verifice dacă un cuvânt este palindrom.
137. Să se transforme un şir din litere mici în litere mari.
138. Să se transforme un şir din litere mari în litere mici.
139. Se citeste un text dintr-un fisier si un caracter c. Sa se determine de cate ori se gaseste caracterul in text (nu se face distinctie intre literele mari si literele mici).
140. Se citeste un text de la tastatura astfel incat cuvintele sa fie separate printr-un singur spatiu si imediat dupa ultimul cuvant se scrie punct. Textul va fi scris pe un singur rand.
a) Sa se determine cate cuvinte contine textul. De ex : "Ana are mere." Contine 3 cuvinte.
b) Sa se determine daca textul are cuvinte distincte (se ignora diferenta de cheie).
c) Sa se determine daca textul contine cifre.
141. Sa se determine de cate ori se gaseste un cuvant intr-un text.
142. Codificati un text astfel incat litera a sa devina c, b sa devina e s.a.m.d.
143. Simulati comanda REPLACE astfel incat intr-un text veti inlocui un caracter x citit de la tastatura cu un alt caracter y citit de la tastatura. Se ignora sau nu diferenta de cheie dupa optiunea utilizatorului.
144. Simulati comanda REPLACE astfel incat intr-un text veti inlocui un sir x citit de la tastatura cu un alt caracter sir y citit de la tastatura. Se ignora sau nu diferenta de cheie dupa optiunea utilizatorului.
145. Se citeste de la tastatura un cuvant. Sa se stabileasca daca el contine doua litere alaturate identice, afisandu-se un mesaj corespunzator.
146. Dintr-un fisier se citesc numele a n persoane. Sa se modifice continutul fisierului astfel incat toate numele sa fie scrise astfel: prima litera mare si restul litere mici.
147. Sa se ordoneze n siruri dupa lungimea lor.
148. Se citesc n siruri. Pentru fiecare sir se va determina suma codurilor ASCII.
149. Intr-un fisier se scriu numele, prenumele si media elevilor dintr-o clasa. Sa se afiseze elevul cu media cea mai mare.
150. Intr-un fisier sunt scrise cuvinte pe linii separate. Sa se afiseze cuvintele care contin majuscule.
151. Intr-un fisier sunt scrise pe randuri diferite numele a n copii. Sa se modifice continutul fisierului astfel incat sa contina numele ordonate crescator.
152. Sa se afiseze vocalele unui cuvant.
153. Sa se afiseze cuvintele care incep si se termina cu consoana, (vocala) etc.
154. Codificati pasareste un cuvant (un text).
155. Să se despartă un text în cuvinte şi să se afişeze cuvintele separate. Să se afişeze cuvântul de lungime maximă.
156. Să se verifice dacă două cuvinte sunt sau nu anagrame.
157. Să se determine frecvenţa de apariţie a unui caracter într-un text.
158. Să se numere apariţiile unui cuvânt într-un text.
159. Să se genereze toate prefixele / sufixele unui cuvânt.
160. Să se înlocuiască peste tot într-un text un cuvânt cu alt cuvânt.
161. Să se sorteze alfabetic un şir de cuvinte (eventual, fără a distinge literele mici de cele mari).
162. Intr-un text exista un cuvant. Codificati/decodificati cuvantul dupa un algoritm generat de voi.
163. Aceeasi problema pentru un text.
164. Codificarea păsărească a unui cuvânt.
165. Decodificarea unui cuvânt codificat în păsărească. Se va face o validare a cuvântului, iar dacă a fost greşit codificat, se va da un mesaj de eroare.
166. Se dau două texte. Să se stabilească o vocală comună celor două texte, care apare de cele mai puţine ori.
167. Dintr-un fisier se citeste un text. Textul contine cuvinte separate printr-un spatiu. Sa se determine cate cuvinte contine textul.
168. Dintr-un fisier se citeste un text. Sa se determine cate cuvinte are fiecare linie.
169. Se citesc n cuvinte. Sa se afiseze cuvintele care rimeaza.
170. Se citesc cuvinte pana la citirea cuvantului "stop". Sa se afiseze cate dintre cuvintele citite sunt egale cu primul cuvant citit.
171. Se citesc numere naturale mai mici decat 1000. Sa se afiseze pe litere numerele citite.
172. Dintr-un fisier se citeste un text. Textul contine cuvinte separate printr-un spatiu. Se va genera un nou text care va contine cuvintele ordonate alfabetic
173. Dintr-un fisier se citeste un text. Textul contine cuvinte separate printr-un spatiu. Sa se scrie intr-un alt fisier , pe linii separate, fiecare cuvant care apare in text urmat de un numar care va reprezenta de cate ori apare cuvantul in text. Sa se determine cuvantul care apare de cele mai multe ori.
174. Dintr-un fisier se citeste un text. Textul contine cuvinte separate printr-un spatiu. Intr-un alt fisier se va scrie pe linii separate fiecare cuvant si liniile pe care apare.
175. Dintr-un fisier se citeste un text. Textul contine cuvinte separate printr-un spatiu sau mai multe. Se va genera un nou fisier care va contine textul initial avand spatiile de prisos eliminate (intre cuvinte va ramane numai cate un spatiu).
176. Simulati scrierea unei parole intr-un fisier. La tastarea parolei pe ecran in locul fiecarui caracter se va scrie caracterul '*'. Eventual realizati si incriptarea parolei inainte de a fi scrisa intr-un fisier.
TIPUL ÎNREGISTRARE (ARTICOL)
177. Într-o clasă sunt n elevi, iar pentru fiecare se citeşte numele, notele obţinute la o materie şi nota la teză. Să se calculeze mediile elevilor. Să se afişeze numele elevilor care au obţinut media maximă. Să se afişeze elevii în ordinea alfabetică a numelor. Să se afişeze apoi în ordinea descrescătoare a mediilor. Să se afişeze elevii corigenţi.
178. Se citesc n ţări, însoţite de culorile drapelelor lor. Se citeşte apoi o anumită culoare. Să se afişeze numele ţărilor care au în componenţe drapelului acea culoare. Se va introduce pentru fiecare ţară numărul de culori al drapelului.
179. Se citesc n segmente date prin coordonatele punctelor care le formează. Să se calculeze lungimile segmentelor. Să se afişeze coordonatele segmentului de lungime maximă.
180. Să se calculeze suma, diferenţa, produsul şi raportul a două numere complexe. Numerele şi rezultatele afişate vor fi de forma Re+i Im.
181. Realizaţi un program care să afişeze elevii admişi la un liceu, în urma concursului de dosare.
182. Realizaţi un program în sprijinul calculării şi afişării rezultatelor elevilor unei şcoli la examenul de bacalaureat.
183. Într-o bibliotecă sunt n cărţi. Pentru fiecare se citeşte titlul, autorul, preţul. Să se afişeze cărţile în ordinea titlurilor. Să se afişeze toate cărţile scrise de un anumit autor, al cărui nume se citeşte de la tastatură. Să se afişeze titlul şi autorul cărţii celei mai scumpe (dacă sunt mai multe cărţi de preţ maxim, se vor afişa toate). Să se listeze cărţile în ordinea descrescătoare a preţurilor.
184. Într-un magazin sunt n produse. Pentru fiecare se citeşte de la tastatură numele produsului, preţul unitar şi numărul de bucăţi vândute şi se calculează preţul total de vânzare. Să se afişeze numele produsului celui mai scump. Să se calculeze media aritmetică a preţurilor unitare. Să se afişeze produsele în ordinea alfabetică a numelor.
185. Se citesc n numere naturale. Să se calculeze pentru fiecare numărul divizorilor proprii şi suma cifrelor. Să se afişeze numerele cu cei mai mulţi divizori proprii. Să se afişeze numerele cu suma cifrelor minimă.
186. Se citesc n numere naturale. Să se afişeze în ordinea descrescătoare a numărului de divizori proprii.
187. Se citesc n numere naturale. Să se calculeze pentru fiecare inversul şi suma factorialelor cifrelor. Să se afişeze numerele şi inversele lor. Să se afişeze numerele cu suma factorialelor cifrelor minimă.
Grafuri orientate
188. Sa se parcurga un graf in latime incepand de la fiecare varf.
189. Sa se determine daca exista varfuri in graf de la care incepand se poate parcurge intreg graful. Care sunt varfurile respective.
190. Se stie ca un graf orientat retine un arbore genealogic astfel incat se porneste de la doi stramosi comuni si descendentii acestora. Din fisierul arbgn.in se citesc : n, numarul persoanelor din arboreal genealogic, numarul de relatii m de forma ascendant – descendent (numarul de arce) iar in continuare m perechi numerice corespunzatoare ascendentului si descendentului urmate de perechile de nume corespunzatoare. Sa se determine care sunt cei 2 stramosi comuni din arborele genealogic si pentru fiecare sa se afiseze in ordine descendentii (parcurgere in latime).
191. Aceeasi problema cu diferenta ca din fisier se citesc n, m si m perechi de nume. Cate generatii contine arboreal genealogic?
192.
*Un
eschimos locuieste la iglul cu numarul z. El are o harta pe care sunt marcate
iglu-urile din zona (numerotate de la 1 la n) si distantele dintre acestea.
Stiind ca din cauza frigului eschimosul nu poate sa parcurga o distanta mai
mare de 20 km fara oprire, afisati o varianta de a ajunge la prietenul lui care locuieste la iglul cu
numarul w. Cati kilometri a parcurs
eschimosul?
193.
Sa se determine daca un graf orientat contine circuite
194.
Matricea
a(nxn) drumurilor unui graf cu n varfuri este o matrice booleana cu a[i][j]=1
daca exisat drum de la I la j si 0 daca nu exista drum de la I la j. Sa se
genereze matricea drumurilor unui graf orientat citit din fisier.
195.
Sa se determine :
a) succesorii unui nod x
b) predecesorii unui nod
x
196.
Sa se
determine componente tare conexa careia ii apartine un varf
197.
Sa se
determine daca un graf este tare conex (numarul de componente tare conexe sa
fie egal cu 1) .
198.
Intr-o
localitate , intre cele n repere, exista o retea de m stradute cu sens
unic avand lungime egala. Care este
numarul minim de stradute ce trebuie parcurse intre reperul x si reperul y?
199.
*Elevii
unei clase au de scris o compunere . Deoarece doresc sa se inspire unii de la
altii, ei isi imprumuta unii altora caietele de teme. SE cunoscperechile de
elevi (numerotati de la 1 la n) care si-au imprumutat caietele. Scrieti un
program care sa determine?
a) la cati elevi a imprumutat (direct)
elevul x. Care sunt acei elevi?
b) de la cati elevi a imprumutat caietul elevul x. Care sunt acei elevi?
c) ce lungime are inlantuirea minima de imprumuturi astfel incat caietul sa ajunga de la x la y? (alg. Lui Lee).
d) tema carui elev a inspirit cele mai multe teme?
200.
Lantul
slabiciunilor
Grafuri neorientate
201.
Un graf
neorientat citit din fisier: nr de muchii, nr de noduri si muchiile:
a)
sa se
memoreze utilizand matrice de adiacente
b)
liste de
adiacente
c)
sa se
parcurga df
d)
sa se
parcurga bf
202.
Sa se
genereze un graf neorientat cu n noduri si sa se afiseze matricea de adiacente
203.
Fie un
graf neorientat citit din fisier
a)
Sa se
parcurga graful in adancime incepand cu nodul 1
b)
Sa se determine
daca graful este conex
c)
Sa se
determine cate componente conexe are graful
d)
Sa se
afiseze care este componenta conexa careia ii apartine un nod x
e)
Sa se
afiseze graful pe componente conexe
204.
Un graf
neorientat este bipartit daca exista o partitie a multimii nodurilor in doua
multimi A si B astfel incat oricare doua varfuri din aceeasi multime sa nu fie
adiacente. Sa se scrie un program care verifica daca un graf este bipartit si
in caz afirmativ sa se tipareasca multimile A si B
Recursivitate
205. Cel mai mare divizor comul a 2 numere
206. Elementul n din sirul lui Fibonacci
207. n factorial
208. suma primelor n numere
209. Expresii:
1x2+2x3+3x4+....+nx(n+1)
˝+2/3+3/4+......+n/(n+1)
210. Sa se afiseze cifrele unui numar incepand de la unitati
211. Sa se determine suma cifrelor unui numar
212. Sa determine cifra cea mai mare a unui numar
213. sa se determine suma cifrelor pare ale unui numar
214. sa se afiseze divizorii unui numar
215. Sa se numere divizorii unui numar
216. sa se determine suma divizorilor unui numar
217. Sa se determine daca un numar este prim
218. *un cioban isi cumpara oi. stiind ca o oaie dupa un an face o mieluta si mieluta devine dupa un an mioara iar mioara devine dupa un an oaie, ce va contine turma ciobanului dupa n ani?
Obs. Nu se nasc berbecuti si nici nu mor animale
dupa un an:
1 oaie si o mileluta nici o mioara
dupa doi ani:
o oaie, o mieluta si o mioara
dupa 3 ani:
2 oi,1 mioara , mielut 1
dupa 4 ani
3 oi, 1 mioara, 2 mieluti
Divide et Impera
219. Suma elementelor unui vector
220. Fie un v vector de numere intregi. Sa se determine valoarea expresiei:
a)v[1]+2v[2]2+3v[3]3+.....+nv[n]4
b)(1+v[1])(1+v[2])......(1+v[n-1])(1+v[n])
221. Minimul (maximul) elementelor dintr-un vector
222. Cel mai mare divizor comun al elementelor dintr-un vector
223. Cautarea binara
224. Sortarea rapida (Quick Sort)
225. Sortarea prin interclasare
226. Turnurile din Hanoi
227.
*n copii culeg mere . Sa se
determine:
a) copilul care a cules cele mai multe mere
b)copii care au cules mai mult de x mere si numarul lor
c)daca sunt copii care au cules acelasi
numar de mere
d)ordonati crescator copii dupa nr de mere culese folosind D et I
e)numarul de mere culese in total
228. tabla impuscata
Backtracking
229. Problema permutarilor primelor n numere
230. Problema aranjamentelor
231. Problema combinarilor
232. Problema permutarilor, combinarilor, aranjamentelor de numere.
233. Problema damelor
234. Problema turelor
235. Pe o tabla de dimensiune nxn se gasesc n regi. Sa se gaseasca toate posibilitatile de aranjare a regilor pe tabla astfel incat oricare 2 regi sa nu se atace. Obs. Fiecare rege se va gasi pe alta linie.
236. Problema partitiilor unui numar
237. Submultimile unui numar
238. Sa se genereze toate drapelele tricolore care se pot forma cu n culori (eventual impunand conditii : in mijloc sa fie o anumita culoare, o culoare sa nu stea langa alta culoare etc
239. <SPAN lang=FR style="mso-ansi-language: FR">Produsul cartezian<SPAN style="mso-spacerun: yes"> </SPAN>a 2 / n multimi
240. <SPAN lang=FR style="mso-ansi-language: FR">Produsul cartezian<SPAN style="mso-spacerun: yes"> </SPAN>a n multimi impunand conditia ca suma elementelor dintr-o solutie sa fie egala cu un S citit
241. <SPAN lang=FR style="mso-ansi-language: FR">Sa se afiseze toate submultimile de cardinal m care se pot forma cu elementele unei multimi cu n elemente (eventual impunand conditia ca suma elementelor dintr-o solutie sa fie egala cu S) Varianta : nr apartin{1,2…n} Ordinea elementelor in solutie este / nu este importanta
242. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate cuvintele binare de lungime n
243. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate functiile f :{1,2…m}-></SPAN><SPAN lang=FR style="FONT-FAMILY: Wingdings; mso-ansi-language: FR; mso-ascii-font-family: 'Times New Roman'; mso-hansi-font-family: 'Times New Roman'; mso-char-type: symbol; mso-symbol-font-family: Wingdings"><SPAN style="mso-char-type: symbol; mso-symbol-font-family: Wingdings"></SPAN></SPAN><SPAN lang=FR style="mso-ansi-language: FR"> {1,2…n}
244. <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate functiile injective f :{1,2…m}</SPAN><SPAN lang=FR style="FONT-FAMILY: Wingdings; mso-ansi-language: FR; mso-ascii-font-family: 'Times New Roman'; mso-hansi-font-family: 'Times New Roman'; mso-char-type: symbol; mso-symbol-font-family: Wingdings"><SPAN style="mso-char-type: symbol; mso-symbol-font-family: Wingdings">-></SPAN></SPAN><SPAN lang=FR style="mso-ansi-language: FR"> {1,2…n}
245. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate functiile bijective f :{1,2…n}-></SPAN><SPAN lang=FR style="FONT-FAMILY: Wingdings; mso-ansi-language: FR; mso-ascii-font-family: 'Times New Roman'; mso-hansi-font-family: 'Times New Roman'; mso-char-type: symbol; mso-symbol-font-family: Wingdings"><SPAN style="mso-char-type: symbol; mso-symbol-font-family: Wingdings"></SPAN></SPAN><SPAN lang=FR style="mso-ansi-language: FR">{1,2…n}
246. <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate submultimile de cate k elemente care se pot forma cu numerele 1,2…n (sau a[1],a[2]…a[n]), cu conditia ca fiecare element sa fie divizibil cu un numar d dat.
247. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se rearanjeze elementele unui vector a[1],a[2]…a[n] in toate modurile posibile, astfel incat oricare doua alaturate sa nu fie consecutive in sirul initial
248. <SPAN lang=FR style="mso-ansi-language: FR">Sa se aranjeze n margele de m culori astfel incat oricare doua margele alaturate sa aiba culori diferite
249. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate numerele de lungime p care sunt supermultiple de p (atat numerele cat si toate prefixele lor sa fie multiplu de p)</SPAN>
250. </SPAN><SPAN lang=FR style="mso-ansi-language: FR">La un festival de muzica usoara s-au inscris n melodii codificate cu numere de la 1 la n. Stiind ca in prima zi intra in concurs k melodii, sa se afiseze toate posibilitatile de a stabili ordinea intrarii in concurs a melodiilor in prima zi, stiind ca melodiile de coduri c1 si c2 trebuie sa intre in prima zi, a doua respectiv penultima
251. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se afiseze toate numerele de lungime p<=9<SPAN style="mso-spacerun: yes"> </SPAN>cu proprietatea ca au suma cifrelor egala cu x dat
252. <SPAN lang=FR style="mso-ansi-language: FR">Sa se afiseze toate submultimile cu p elemente dintre elementele a[1],a[2]…a[n] cu proprietatea ca suma elementelor din multime este un numar divizibil cu x dat
253. <SPAN lang=FR style="mso-ansi-language: FR">Sa se afiseze toate modurile in care se poate forma un grup de p persoane dintr-un grup de n persoane, dintre care l persoane sa fie femei
254. </SPAN><SPAN lang=FR style="mso-fareast-font-family: 'MS Mincho'; mso-ansi-language: FR"></SPAN><SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate cuvintele de lungime p, distincte / nedistincte, care se pot forma cu literele alfabetului dintr-o multime data
255. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se aranjeze in toate modurile elementele unui vector a[1],a[2]…a[n] formand perechi de lungime p, astfel incat fiecare element sa apara de cel mult doua ori</SPAN>
256. </SPAN> <SPAN lang=FR style="mso-ansi-language: FR">La un concurs se prezinta n concurenti din m tari. Sa se stabileasca ordinea intrarii in concurs a celor n concurenti astfel incat doi concurenti din aceeasi tara sa nu urmeze unul dupa altul</SPAN>
257. <SPAN lang=FR style="mso-ansi-language: FR">Sa se aranjeze elementele multimii {A,R,G,V} in grupuri de cate n (n par) astfel incat doua caractere identice sa nu fie alaturate si R sa apara de exact n/2 ori
258. <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate numerele de lungime n formate doar cu cifre pare / impare
259. <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate numerele de lungime n divizibile cu x dat
260. <SPAN lang=FR style="mso-ansi-language: FR">Sa se determine toate numerele de lungime n care sunt egale cu inversele lor
261. <SPAN lang=FR style="mso-ansi-language: FR">Sa se determine toate modurile in care poate fi capsat un bilet, stiind ca pozitiile posibile sunt de forma:
<SPAN lang=FR style="mso-ansi-language: FR"><SPAN style="mso-spacerun: yes"></SPAN>* * *</SPAN>
<SPAN lang=FR style="mso-ansi-language: FR"><SPAN style="mso-spacerun: yes"></SPAN>* * *</SPAN>
<SPAN lang=FR style="mso-ansi-language: FR"><SPAN style="mso-spacerun: yes"></SPAN>* * *</SPAN>
Biletul poate fi introdus pe oricare din fete.
262.
Sunt 2n
copii de inaltimi diferite. Sa se aseze copiii pe 2 randuri astfel:
<SPAN lang=FR
style="mso-ansi-language: FR"><SPAN style="mso-spacerun:
yes"></SPAN>- pe primul rand copiii sa fie asezati
in ordinea crescatoare a inaltimii
</SPAN><SPAN lang=FR
style="mso-ansi-language: FR"><SPAN style="mso-spacerun:
yes"></SPAN>- copiii de pe al doilea rand sa fie
mai inalti decat cei din fata lor
263. Sa se genereze toate solutiile naturale nenule ale ecuatiei 4x+y+3yz=100
264. <SPAN lang=FR style="mso-ansi-language: FR">Sa se genereze toate numerele naturale ale caror cifre se gasesc printre cifrele lui x citit si au lungimea cel mult egala cu lungimea lui x. Cifrele se pot repeta</SPAN>
265. <SPAN lang=FR style="mso-ansi-language: FR">La Masa Rotunda sunt n cavaleri. Fiecare dintre ei are cel putin un dusman rpintre ceilalti. Sa se gaseasca toate posibilitatile de a-i aseza la masa astfel incat doi vavaleri dusmani sa nu fie vecini. Se citesc cele m perechi de dusmani de la tastatura (fisier)
266. <SPAN lang=FR style="mso-ansi-language: FR">Fie X=(X1,X2...Xn) un vector cu componente distincte. Sa se determine toate subsirurile (Xi1,Xi2...Xip) cu proprietatea ca i1<i2<...<ip si Xi1<Xi2<...<Xi</SPAN>
<SPAN lang=FR style="mso-ansi-language: FR">Sa se gaseasca toate reprezentarile posibile ale lui n ca suma de nr consecutive (nu e eficienta tehnica backtracking)<o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Partitiile unui nr natural in numere prime / pare / divizibile cu d / alte conditii<o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Sa se afiseze toate numerele formate din cifre distincte cu proprietatea ca suma cifrelor este egala cu S (ex : S=3 </SPAN><SPAN lang=FR style="FONT-FAMILY: Wingdings; mso-ansi-language: FR; mso-ascii-font-family: 'Times New Roman'; mso-hansi-font-family: 'Times New Roman'; mso-char-type: symbol; mso-symbol-font-family: Wingdings"><SPAN style="mso-char-type: symbol; mso-symbol-font-family: Wingdings">ŕ</SPAN></SPAN><SPAN lang=FR style="mso-ansi-language: FR"> 102, 12, 120, 201, 21, 3, 30)<o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Patronul unei echipe de fotbal doreste sa achizitioneze noi jucatori. Cunoscand suma S avuta la dispozitie de acesta precum si sumele cerute de cluburile la care sunt titulari jucatorii doriti, sa se afiseze toate modalitatile de cumparare a jucatorilor, incadrandu-se exact in suma avuta la dispozitie (varianta : Sa nu se incadreze exact in suma ; Sa cumpere cat mai multi jucatori – Greedy)<o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Să se genereze toate numerele naturale ale căror cifre se găsesc printre cifrele lui x citit şi au lungimea cel mult egală cu lungimea lui x<o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Se dau n cifre distincte v1,v2...vn. Sa se gaseasca toate numerele nenule mai mici decat un numar A care se pot forma cu cifrele v1...vn<o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Fie X=(X1,X2...Xn) un vector cu componente distincte. Sa se determine toate subsirurile (Xi1,Xi2...Xik), k>=2, cu proprietatea ca i1<i2<...<ik si Xi1<Xi2<...<Xik <o:p</o:p</SPAN> <SPAN lang=FR style="mso-ansi-language: FR">Fie X=(X1,X2...Xn) un vector cu componente distincte. Sa se determine toate subsirurile de lungime maxima (Xi1,Xi2...Xik) cu proprietatea ca i1<i2<...<ik si Xi1<Xi2<...<Xik<o:p</o:p</SPAN>
267.
268.
269.
270. Plata unei sume in bancnote de n tipuri. Solutia cea mai lunga (scurta)
271. Sa se genereze n perechi de acolade care se inchid corect
272. Sa se genereze toate numerele palindrome de lungime n
273. Problema drapelelor. Sa se afiseze ca drapel
274. Sa se genereze anagramele unui cuv
275. Sa se genereze toate numerele palindrome de lungime n
276. Sa se genereze toate triunghiurile de perimetru n
277. Intre n persoane care stau pe scaune s-au iscat conflicte. Acestea stau pe scaune numerotate de la 1 la n. Scrieti un program care sa afiseze toate modurile posibile de reasezare a persoanelor astfel incat sa nu se gaseasca alaturi doua persoane in conflict.
278. La o cofetarie se comercializeaza n sortimente de prajituri. Sa se determine toate variantele de a face pachete cu cate p prajituri diferite. Scrieti un program care permite citirea de la tastatura a celor n sortimente de prajituri si afiseaza variantele solutie precum si numarul acestora.
279. Fiind data o multime de n cuburi, fiecare cub fiind caracterizat de lungimea laturii si culoarea sa, sa se scrie un program care sa genereze toate turnurile care se pot forma cu p cuburi astfel incat doua cuburi vecine sa nu aiba aceeasi culoare iar deasupra unui cub sa nu se poata aseza un cub cu latura mai mare.
280. Scrieti un program care sa afiseze toate numerele de trei cifre, formate numai din cifre distincte si care sunt divizibile cu 4.
281. Un grup de copii are la dispozitie n cartonase cu n cuvinte disticte pentru jocul "cerc de cuvinte". In acest joc un copil trebuie sa spuna un cuvant care sa aiba primele doua litere identice cu ultimele doua ale cuvantului spus de predecesorul lui. fiind dat un cuvant de inceput pentru joc, afisati varianta cu cele mai multe cuvinte care se pot obtine cu ajutorul cartonaselor date. Observatie: un sir de cuvinte nu va contine un cuvant de mai multe ori.
282. Gigel are n cartonase (n<=10). Pe fiecare este scrisa o cifra de la 1 la 9. Uilizand doua tipuri de cartonase cu + si - vrea sa obtina rezultatul 2. Care sunt solutiile pentru n citit?
283. O persoana a uitat numarul de telefon al unui prieten. Stiedoar ca numarul are 6 cifre, incepe cu 4 si contine 3 zerouri dintre care doua sunt alaturate. fisati toate variantele pe care trebuie sa le incerce pentru a vorbi cu prietenul sau.
284. La o masa rotunda sunt n persoane de diverse nationalitati, pentru fiecare persoana precizandu-se doua limbi straine cunoscute de ea. Se cere sa ajutati organizatorii mesei rotunde sa aranjeze persoanele astfel incat fiecare sa poata conversa atat cu cea din stanga cat si cu cea din dreapta.
285. Sa se genereze numerele mai mici decat n citit care trecute in baza 2 au in componenta lor exact p cifre de 1.
286. Sa se determine suma tuturor numerelor cu cifre distincte. Cate astfel de numere sunt?
287. 6 din 49
288. Pronosport
289. Sa se genereze toate triunghiurile avand suma lungimilor laturilor egala cu n (n natural si lungimi naturale)
290. SE va citi un numar n natural de la tastatura. Sa se genereze toate numerele avand p cifre pare ele lui n
291. Sa se genereze toate matricile binare (avand 0 si 1) simetrice cu nxn componente.
292. Sa se genereze o secventa de n sunete avand lungimea p care respecto o anumita conditie
293. La un spectacol trebuie sa interpreteze cate o poezie copiii A, B, C, D, E astfel incat copilul D sa recite inainte de A si B. Sa se genereze toate posibilitatile de recitare a poeziilor.
294. Intr-un sir indian se gasesc n copii. Sa se genereze toate posibilitatile de rearanjare a copiilor astfel incat in noua configuratie fiecare copil sa se gaseasca dupa un copil diferit de copilul care se situa in configuratia initiala.
295.
Sa se decompuna un numar in suma
de numere prime. Generati toate solutiile.
Arbori
Arbori oarecare
296. Fie un graf neorientat citit din fisier. Sa se determine daca graful poate fi arbore.
297. Fie un graf neorientat memorat prin matricea de adiacente. Se stie ca graful poate fi si arbore. Sa se memoreze arborele prin legaturi de tip tata. Radacina se citeste de la tastatura.
298. Fie un arbore de memorat prin legaturi de tip tata.
a) Sa se determine nodul radacina
b) Sa se determine nodurile terminale
c) Sa se afiseze pentru fiecare nod predecesorii si nivelul pe care se gaseste
d) Care este adancimea arborelui?
299. Fie un arbore de memorat prin legaturi de tip tata. Sa se afiseze nodurile de pe nivelul x.
300. Intr-un fisier sunt memorate n numere naturale. Intre cele n numere se stabileste o relatie de tip arbore oarecare. In fisier sunt scrie pe prima linie n, pe linia a doua cele n valori iar pe linia a treia vectorul de tip tata asociat. Sa se determine suma cifrelor numerelor asociate incepand de la un nod pana la radacina. Nodul de pornire se citeste de la tastatura.
Exemplu:
7
12 14 15 25 430 82 91 cele 7 numere
0 1 1 3 3 1 5
se citeste nodul 5
Se afiseaza 16
301. Intr-un fisier sunt memorate numele a n persoane. Intre cele n persoane se stabileste o relatie de tip arbore oarecare (arbore genealogic cu un stramos comun) . In fisier sunt scrie pe prima linie n, pe linia a doua cele n nume iar pe linia a treia vectorul de tip tata asociat. Sa se afiseze parintele si fratii unei persoane (se citeste de la tastatura numele acesteia).