Algoritmul lui
Djikstra
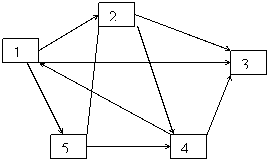
Fie G=(V,
E) un graf orientat, unde V are n elemente (n varfuri) si E are m elemente
(m arce). Se cunosc costurile arcelor.
Matricea
costurilor: 0 1 9 ∞ 3 ∞ 0 7 3 ∞ ∞ ∞ 0 ∞ ∞ 1 ∞ 2 0 ∞ ∞ 4 ∞ 2 0
1 7
4 3
9
3 1 2
2
Ne
propunem sa determinam costul minim de la un varf la toate celelalte varfuri.
Fie acesta varful 1.
Vom utiliza 3 vectori :
- Vectorul d care va retine lungimea drumurilor de la
1 la celelalte varfuri. (d[i]=lungime drum de la 1 la i). Initial d
retine :
|
0 |
1 |
9 |
∞ |
3 |
- Vectorul s, numit vector caracteristic va retine 1
pentru nodurile selectate ca participante la drumul minim, altfel s retine
0. Initial va retine 1 doar pentru varful de pornire , in cazul nostru
varful 1
|
1 |
0 |
0 |
0 |
0 |
- Vectorul t , vector de tip tata care va indica
drumurile gasite intre varful 1 si celelalte varfuri astfel incat pentru
fiecare varf se va retine precedentul (tatal). Pentru varful de
pornire, 1 in cazul nostru, se retine 0. Initial t va retine :
|
0 |
1 |
1 |
0 |
1 |
Algoritmul :
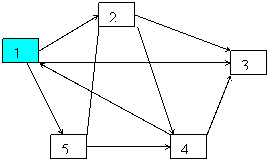
- Se porneste de la varful 1(r=1, unde r are
valoare de radacina) . Se marcheaza in s cu 1 : s[r]=1
Matricea
costurilor: 0 1 9 ∞ 3 ∞ 0 7 3 ∞ ∞ ∞ 0 ∞ ∞ 1 ∞ 2 0 ∞ ∞ 4 ∞ 2 0
1 7
4 3
9
3 1 2
2
In vectorul d se incarca costurile de la
r la fiecare dintre celelalte varfuri
Vectorul
d :
|
0 |
1 |
9 |
∞ |
3 |
Vectorul s :
|
1 |
0 |
0 |
0 |
0 |
Vectorul t :
|
0 |
1 |
1 |
0 |
1 |
- Pentru varurile ramase, deci de n-1 ori se
executa secventa :
Se determina cel mai apropiat varf de
varful 1 din vectorul d (valoarea minima din d) :
|
0 |
1 |
9 |
∞ |
3 |
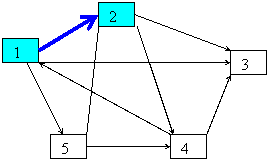
Acesta este
varful 2 care se adauga la drum :
:
1 7
4 3
9
3 1
2
2
min=1, vf=2
se marcheaza in s :
Vectorul s :
|
1 |
1 |
0 |
0 |
0 |
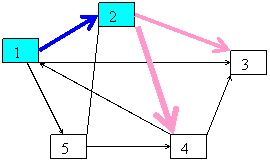
In continuare se pune problema daca
pentru nodurile neadaugate inca nu s-ar putea realiza imbunatatiri ale lungimii
drumurilor prin 2:
Adica pentru un varf x daca
d[x]>d[vf]+a[vf][x] atunci re realizeaza modificarea efectiv in d si se
adauga vf ca fiind predecessor (tata) pentru x:
if(d[x]>d[vf]+a[vf][x])
{ d[x]=d[vf]+a[vf][x];
t[x]=vf;
}
1 7
4 3
9
3 1 2
2
Se pot imbunatati drumurile de la 1 la 3
prin 2 si de la 1 la 4 prin 2. Vectorii devin :
Vectorul
d :
|
0 |
1 |
8 |
4 |
3 |
Vectorul s :
|
1 |
1 |
0 |
0 |
0 |
Vectorul t :
|
0 |
1 |
2 |
2 |
1 |
Mai sunt de adaugat varfurile 3,4, 5.
Acestea se pot « agata » de varfurile adaugate (selectate) fie 1 fie
2.
Se procedeaza la fel : se determina
cel mai apropiat varf : min =3 si vf=5
Vectorul
d :
|
0 |
1 |
8 |
4 |
3 |
Se selecteaza in
s : s[vf]=1:
Vectorul s :
|
1 |
1 |
0 |
0 |
1 |
Dar nu se mai pot obtine imbunatatiri
ale drumurilor de la 1 la varfurile
ramase (3 sau 4) care sa treaca prin 5 prin urmare vectorul t ramane
acelasi :
Vectorul t :
|
0 |
1 |
2 |
2 |
1 |
Am afuns la urmatoarea situatie :
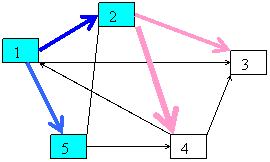
1 7
4 3
9
3 1 2
2
Mai sunt de adaugat varfurile 3 si
4. Varfurile adaugate sunt 1 ,2 si 5
Se cauta in continuare cel mai apropiat
varf neselectat inca(pentru care in s valoarea este 0). Acesta este 4 :
Min=4, vf=4.
Se adauga la arbore si se obtine :
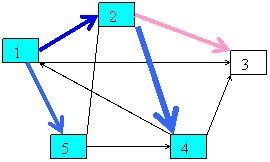
1 7
4 3
9
3 1 2
2
Se poate realiza o imbunatatire a
drumului de la 1 la 3 prin 4 si se adauga 4
ca parinte pentru
3 iar d[3]=d[4]+a[4][3]=4+2=6
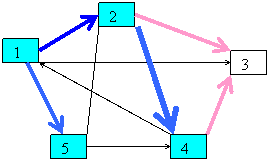
1 7
4 3
9
3 1 2
2
Vectorii devin:
Vectorul
d :
|
0 |
1 |
6 |
4 |
3 |
Vectorul s :
|
1 |
1 |
0 |
1 |
1 |
Vectorul t :
|
0 |
1 |
4 |
2 |
1 |
La sfarsit se adauga varful 3:
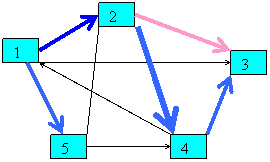
1 7
4 3
9
3 1 2
2
Practic se obtine arborele (un graf
partial):

 1
1
3 1
3

![]()
3 2
4 5
Vectorii devin :
Vectorul
d :
|
0 |
1 |
6 |
4 |
3 |
Vectorul s :
|
1 |
1 |
0 |
1 |
1 |
Vectorul t :
|
0 |
1 |
4 |
2 |
1 |
O solutie de implementare :
#include<fstream.h>
#include<conio.h>
const pinf=1000;
int a[20][20],n,m;
int r;//varful de
inceput
int
s[100];//vectorul caracteristic - marcheaza cu 1 varfurile selectate
int
d[100];//vectorul lungimii drumurilor de la varful r la toate celelelte varfuri
int t[100];//vectorul de tip tata-
pentru
void citire_cost()
{fstream f;
int i,j,x,y,c;
f.open("roy.in",ios::in);
if(f)
cout<<"deschiderea a
reusit";
else
cout<<"eroare la deschidere!";
cout<<endl;
f>>n>>m;
//initializare
matrice
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
a[i][j]=0;
else
a[i][j]=pinf;
for(i=1;i<=m;i++)
{f>>x>>y>>c;
a[x][y]=c;}
}
void afisare_mat()
{cout<<endl<<"matricea
costurilor"<<endl;
for(int
i=1;i<=n;i++)
{for(int j=1;j<=n;j++)
if(a[i][j]==pinf)
cout<<"pinf ";
else
cout<<a[i][j]<<"
";
cout<<endl;}
}
void
afiseaza_vector(int v[100])
{for(int
i=1;i<=n;i++)
cout<<v[i]<<" ";
cout<<endl;}
void cauta_min(int &vf)//caut varful
cel mai apropiat de r care nu a fost selectat inca
{int min=pinf;
for(int
i=1;i<=n;i++)
if(s[i]==0)
if(d[i]<min)
{min=d[i];
vf=i;}
}
void imbunatatire_drum(int vf)//incerc
sa imbunatatesc drumurile de la r la varfurile neselectate inca prin el
{for(int i=1;i<=n;i++)
if(s[i]==0)
if(d[i]>d[vf]+a[vf][i])
{d[i]=d[vf]+a[vf][i];
t[i]=vf;//il adaug pe vaf ca posibil
parinte pentru i
}
}
void drum(int i)
{if(t[i])
drum(t[i]);
cout<<i<<" ";
}
void main()
{clrscr();
int vf,min;
citire_cost();
afisare_mat();
cout<<"nodul de
inceput?";
cin>>r; //r=1 in exemplu
for(int i=1;i<=n;i++)
if(i!=r)
{d[i]=a[r][i];
if(a[r][i]!=pinf)
t[i]=r;
}
for(i=1;i<=n-1;i++)
{cauta_min(vf);//caut varful cel mai
apropiat de r care nu a fost selectat inca
s[vf]=1;
//il selectez ca fiind vizitat
imbunatatire_drum(vf);//incerc sa
imbunatatesc drumurile de la r la varfurile neselectate inca prin el
}
cout<<endl;
cout<<"vectorul drum:
"<<endl;
afiseaza_vector(d);
cout<<"vectorul critic:
"<<endl;
afiseaza_vector(s);
cout<<"vectorul de tati:
"<<endl;
afiseaza_vector(t);
for(i=1;i<=n;i++)
if(i!=r)
if(t[i]!=0)//daca vectorul a fost
adaugat la arbore
{cout<<"drumul de la
"<<r<<" la "<<i<<" este
:"<<endl;
drum(i);
cout<<endl<<"si are lungimea
"<<d[i]<<endl<<endl;}
else
cout<<"nu exista drum de la
"<<r<<" la "<<i<<endl;
getch();
}
Aplicatie :
/*sa se determine drumul minim de la x
la y cu maxim k noduri impare*/
#include<fstream.h>
#include<conio.h>
const pinf=1000;
int
a[20][20],n,m,k;
int r;//varful de
inceput
int
s[100];//vectorul caracteristic - marcheaza cu 1 varfurile selectate
int
d[100];//vectorul lungimii drumurilor de la varful r la toate celelelte varfuri
int t[100];//vectorul de tip tata-
pentru
void citire_cost()
{fstream f;
int i,j,x,y,c;
f.open("test1.txt",ios::in);
if(f)
cout<<"deschiderea a
reusit";
else
cout<<"eroare la deschidere!";
cout<<endl;
f>>n>>m;
//initializare
matrice
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
a[i][j]=0;
else
a[i][j]=pinf;
for(i=1;i<=m;i++)
{f>>x>>y>>c;
a[x][y]=c;}
}
void afisare_mat()
{cout<<endl<<"matricea
costurilor"<<endl;
for(int
i=1;i<=n;i++)
{for(int
j=1;j<=n;j++)
if(a[i][j]==pinf)
cout<<"pinf ";
else
cout<<a[i][j]<<"
";
cout<<endl;}
}
void
afiseaza_vector(int v[100])
{for(int
i=1;i<=n;i++)
cout<<v[i]<<" ";
cout<<endl;}
void cauta_min(int &vf)//caut varful
cel mai apropiat de r care nu a fost selectat inca
{int min=pinf;
for(int
i=1;i<=n;i++)
if(s[i]==0)
if(d[i]<min)
{min=d[i];
vf=i;}
}
int verific(int i)
{if(t[i])
return i%2+verific(t[i]);
else
return 0;
}
void imbunatatire_drum(int vf)//incerc sa imbunatatesc drumurile de la r la
varfurile neselectate inca prin el
{for(int i=1;i<=n;i++)
if(s[i]==0)
if(d[i]>d[vf]+a[vf][i])
{int x;
x=t[i];
t[i]=vf;
int k1=verific(i)+r%2;
if(k1<=k)
d[i]=d[vf]+a[vf][i];
else
t[i]=x;
}
}
void drum(int i)
{if(t[i])
drum(t[i]);
cout<<i<<" ";
}
void main()
{clrscr();
int vf,min;
citire_cost();
afisare_mat();
cout<<"nodul de
inceput?";
cin>>r;
s[r]=1;
//r=1 in exemplu
cout<<"k=";
cin>>k;
for(int
i=1;i<=n;i++)
if(i!=r)
{d[i]=a[r][i];
if(a[r][i]!=pinf)
t[i]=r;
}
for(i=1;i<=n-1;i++)
{cauta_min(vf);//caut varful cel mai
apropiat de r care nu a fost selectat inca
s[vf]=1;
//il selectez ca fiind vizitat
imbunatatire_drum(vf);//incerc sa
imbunatatesc drumurile de la r la varfurile neselectate inca prin el
}
cout<<endl;
cout<<"vectorul drum:
"<<endl;
afiseaza_vector(d);
cout<<"vectorul critic:
"<<endl;
afiseaza_vector(s);
cout<<"vectorul de tati:
"<<endl;
afiseaza_vector(t);
int y;
cout<<"vf
final=";
cin>>y;
cout<<endl;
if(d[y]==pinf)
cout<<"nu exxista solutie";
else
cout<<"drumul minim cu maxim k
varfuri impare are valoarea "<<d[y];
cout<<endl;
drum(y);
getch();
}