Graf hamiltonian

Fie G=(V, E) un graf neorientat, unde V are n elemente (n noduri) si E are m elemente (m muchii).

Lanţ hamiltonian = un lanţ elementar care conţine toate nodurile unui graf

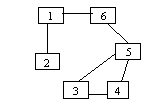L=[2 ,1, 6, 5, 4, 3] este lant hamiltonian

Ciclu hamiltonian = un ciclu elementar care conţine toate nodurile grafului

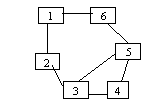C=[1,2,3,4,5,6,1] este ciclu hamiltonian

Graf hamiltonian = un graf G care conţine un ciclu hamiltonian

Graful anterior este graf Hamiltonian.

Problema:

Fiind dat un graf neorientat memorat prin matricea de adiacente sa se determine daca graful este Hamiltonian . In caz afirmativ sa se afiseze ul ciclu Hamiltonian altfel se va afisa un mesaj.

Pentru a rezolva problema vom utiliza tehnica backtracking. Vom incarca in stiva noduri distincte si adiacente, astfel incat pornind de la problema clasica de backtracking a permutarilor vom testa valoarea de pe nivelul k astfel:

· Sa fie un nod adiacent cu precedentul adaugat. E necesar ca: a[st[k-1]][st[k]]=1, in caz contrar se returneaza 0

· Nodul adaugat sa nu se regaseasca pe nivelurile anterioare . Trebuie ca st[k]¹st[i] unde iÎ{1,2…k-1}, in caz contrar se returneaza 0

· Pentru a se incheia ciclul este necesar ca primul si ultimul nod sa fie adiacente. Adica:

a[st[1]][st[n]]=1, in caz contrar se returneaza 0

#include<fstream.h>

#include<conio.h>

#include<stdio.h>

int st[100],n,m,k,a[20][20];

int ns;

//k este este nivelul din stiva (indexul - vetorul solutie),curent

int e_valid()

{if(k>1)

if(!a[st[k-1]][st[k]])

return 0;

else

for(int i=1;i<=k-1;i++)//parcurg nivelurile anterioarenivelului curent

if(st[i]==st[k])

return 0;

if(k==n)

if(!a[st[1]][st[k]])

return 0;

return 1;

}

void afisare()

{for(int i=1;i<=n;i++)

cout<<st[i]<<" ";

cout<<st[1];

k=0; //determina iesirea la prima solutie

ns++;

}

void back()

{k=1; //pe primul nivel initial

while(k>0)//cand k va descreste la 0 algoritmul se incheie

if(st[k]<n)

{st[k]++;

if(e_valid())//daca elementul incarcat este valid

if(k==n)//verific daca am ajuns la solutia completa.

afisare();

else //daca nu am solutia completa urc in stiva (maresc vectorul, adica pe k)

{k++;

st[k]=0;}

}

else

k--;

}

void main()

{clrscr();

fstream f;

f.open("ham.in",ios::in);

int u,v;

if(f)

cout<<"ok!";

else

cout<<"eroare";

cout<<endl;

f>>n>>m;

for(int i=1;i<=m;i++)

{f>>u>>v;

a[u][v]=a[v][u]=1;

}

cout<<"matricea de adiac "<<endl; // afisare matrice de adiacenta

for( i=1;i<=n;i++)

{for(int j=1;j<=n;j++)

cout<<a[i][j]<<" ";

cout<<endl;

}

back();

if(ns==0)

cout<<”nu exista solutii”;

getch();

}