Grafuri
neorientate
Graf neorientat= o pereche de multimi =(V, E)unde V este o mulţime finită nevida de elemente numite noduri
iar E o multime de perechi neordonate din V, numite muchii. Notăm
graful cu G=(V, E).
Intr-un un graf G=(V, E) neorientat relaţia binară
este simetrică: (v,w)ÎE atunci (w,v) ÎE.
Nod = element al mulţimii V, unde G=(V, E) este un graf
neorientat.
Muchie = element al mulţimii E ce descrie o relaţie existentă între două
noduri din V, unde G=(V, E) este un graf neorientat;
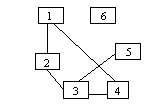
In figura alaturata:
V={1,2,3,4,5,6} sunt noduri
E={[1,2], [1,4], [2,3],[3,4],[3,5]} sunt muchii
G=(V, E)=({1,2,3,4,5,6}, {[1,2], [1,4], [2,3],[3,4],[3,5]})
Adiacenta: Într-un
graf neorientat existenţa muchiei (v,w)
presupune că w este adiacent cu v şi v adiacent cu w.
În exemplul din figura de mai sus vârful 1 este adiacent cu 4 dar 1 şi 3 nu reprezintă o
pereche de vârfuri adiacente.
Incidenţă = o muchie este incidentă cu un nod dacă îl
are pe acesta ca extremitate. Muchia (v,w) este incidentă în nodul v respectiv w.
Grad = Gradul unui nod v, dintr-un graf neorientat, este un număr natural ce
reprezintă numărul de noduri adiacente cu acesta (sau numarul de
muchii incidente cu nodul respectiv)
Nod izolat = Un nod cu gradul 0.
Nod terminal= un nod cu
gradul 1
|
|
Nodul
5 este terminal (gradul 1). Nodul
6 este izolat (gradul 0) Nodurile
1, 2, 4 au gradele egale cu 2. |
Daca un graf neorientat are
m muchii atunci suma gradelor tuturor nodurilor este 2m
In orice graf G exista un numar par de noduri de
grad impar
Lanţ = este o secvenţă de noduri ale unui graf neorientat G=(V,E), cu proprietatea că
oricare două noduri consecutive din secventa lant sunt adiacente:
L=[w1,
w2, w3,. . ,wn] cu proprietatea că (wi,
wi+1)ÎE pentru 1Łi<n.
Lungimea unui lanţ = numărul de muchii din care este
format.
Lanţ simplu = lanţul care conţine numai muchii
distincte
Lanţ compus= lanţul care nu este format numai din
muchii distincte
Lanţ elementar = lanţul care conţine numai noduri
distincte
Ciclu = Un lanţ în care primul
nod coincide cu ultimul.
Ciclul este
elementar dacă este format doar din noduri distincte, excepţie făcând
primul şi ultimul. Lungimea unui ciclu nu poate fi 2.
|
|
Succesiunea
de vârfuri 2,
3, 5, 6 reprezintă un lanţ
simplu şi elementar de lungime 3. Lanţul
5 3 4 5 6 este simplu dar nu este elementar. Lanţul
5 3 4 5 3 2 este compus şi nu este elementar. Lanţul
3 4 5 3 reprezintă un ciclu elementar |
Graf partial = Dacă dintr-un graf G=(V,E) se suprimă cel puţin o muchie atunci noul graf
G’=(V,E’), E’Ě E se numeşte graf
parţial al lui G (are aceleasi noduri si o parte din muchii).


G G1
este graf partial al lui G
Subgraf = Dacă dintr-un graf G=(V,E) se suprimă cel
puţin un nod împreună cu muchiile incidente lui, atunci noul graf G’=(V’,E’), E’Ě E si V’ĚV se numeşte subgraf al lui G.


G G1
este subgraf al lui G
Graf regulat = graf neorientat în care toate nodurile au acelaşi
grad;

Graf complet = graf neorientat G=(V,E) în care există muchie între oricare două
noduri.
Numărul de muchii ale unui graf complet
este: nr*(nr-1)/2.Unde nr este numarul de noduri
 graf
complet. Nr de muchii: 4x(4-1)/2 = 6
graf
complet. Nr de muchii: 4x(4-1)/2 = 6
Graf conex = graf neorientat G=(V,E) în care pentru orice pereche de noduri (v,w) există un lanţ
care le uneşte.
 graf conex
graf conex nu este graf conex
nu este graf conex
Componentă conexă = subgraf al grafului de referinţă, maximal
în raport cu proprietatea de conexitate (între oricare două vârfuri există
lanţ);
 graful nu este
conex. Are 2 componente conexe:
graful nu este
conex. Are 2 componente conexe:
1, 2 si 3, 4, 5, 6
Lanţ
hamiltonian = un lanţ elementar care conţine toate nodurile unui graf
 L=[2 ,1, 6, 5, 4, 3]
este lant hamiltonian
L=[2 ,1, 6, 5, 4, 3]
este lant hamiltonian
Ciclu hamiltonian = un ciclu elementar care conţine toate nodurile
grafului
 C=[1,2,3,4,5,6,1]
este ciclu hamiltonian
C=[1,2,3,4,5,6,1]
este ciclu hamiltonian
Graf hamiltonian = un graf G care conţine un ciclu hamiltonian
Graful anterior este graf Hamiltonian.
Daca G este un graf cu n>=3 noduri astfel
incat gradul fiecarui nod este mai mare sau egal decat n/2 atunci G este
hamiltonian
Lanţ eulerian = un lanţ simplu care conţine toate muchiile
unui graf

Lantul: L=[1.2.3.4.5.3.6.2.5.6] este lant
eulerian
Ciclu eulerian = un ciclu simplu care conţine toate muchiile
grafului
Ciclul:
C=[1.2.3.4.5.3.6.2.5.6.1] este ciclu eulerian
Graf eulerian = un graf care
conţine un ciclu eulerian.
Condiţie
necesară şi suficientă: Un graf este eulerian dacă şi numai
dacă oricare vârf al său are gradul par.
Intrebari si exercitii :
- desenati un graf G neorientat cu 6 noduri si 10 muchii
- Exprimati graful ca o relatie binara detaliind
multimea nodurilor si multimea muchiilor
- precizati pentru fiecare nod gradul
- precizati un lant simplu, un lant compus
- precizati un lant elementar, neelementar
- precizati un ciclu
- desenati un graf Gp partial cu 7 muchii
- desenati un subgraf Gs cu 4 noduri
- modificati Gs astfel incat Gs sa fie graf complet
- desenati un graf regulat Gr cu 9 noduri
- cate componente conexe are Gr?
- modificati Gr astfel incat sa obtineti Gr1 graf conex
- precizati un lant hamiltonian in Gr1
- modificati Gr astfel incat
acesta sa fie graf eulerian
- precizati un ciclu eulerian in Gr
- puteti desena
urmatoarea figura fara a ridica creionul de pe hartie si fara a repete muchiile?
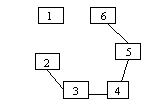
- este graful anterior eulerian ? de ce ?
