Parcurgerea grafurilor in adancime (depth first)

Parcurgerea unui graf in adancime se face prin utilizarea stivei (alocate implicit prin subprograme recursive).

Pentru fiecare varf se parcurge primul dintre vecinii lui neparcursi inca

Dupa vizitarea varfului initial x₁, se exploreaza primul varf adiacent lui, fie acesta x₂ , se trece apoi la primul varf adiacent cu x₂ si care nu a fost parcurs inca , s.a.m.d.

Fiecare varf se parcurge cel mult odata

De exemplul pentru garful din figura de mai jos, se va proceda in felul urmator:

se porneste din varful 1, (se poate incepe de la oricare alt varf)

se exploreaza in continuare primul vecin al acestuia acestuia : varful 2,

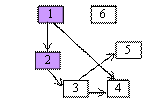se obtine 1,2

dupa care din 2 se exploreaza varful adiacent cu acesta si care nu a fost vizitat : 3.

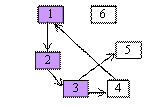se obtine 1,2,3

In continuare ar trebui sa se parcurga vecinul lui 3 nevizitat : 4

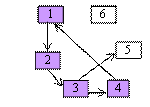se obtine 1, 2, 3, 4

Pentru varful 4 ar trebui sa se parcurga primul sau vecin neparcurs (varful 1 dar acesta a fost deja parcurs. Nu mai avem ce vizita si se trece la nivelul anterior din stiva, la varful 3 :

1, 2, 3, 4 Se parcurge vecinul sau nevizitat, varful 5 .

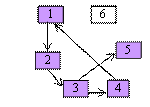SE obtine : 1, 2, 3, 4 , 5.

Varful 3 nu mai are vecini nevizitati si se trece pe nivelul anterior din stiva, varful 2 : 1, 2, 3, 4 , 5. Nici acesta nu mai are vecini nevizitati si se trece pe nivelul anterior la varful 1 : 1, 2, 3, 4 , 5. Cum nici acesta nu mai are vecini nevizitati se incheie algoritmul.

Varful 6 ramane nevizitat.

Algoritmul

-Graful se va memora utilizand matricea de adiacenta a[10][10]

-pentru a nu parcurge un varf de doua ori se va folosi un vector boolean viz care va retine :

- viz[k]=0 daca varful k nu a fost vizitat inca

- viz[k]=1 daca varful k a fost vizitat

-ca si la parcurgerea in latime vecinii unui varf se « cauta » pe linia acestui varf : daca a[nod][k]=1 inseamna ca varfurile nod si k sunt adiacente. Pentru ca varful k sa fie fie parcurs trebuie ca varful sa nu fi fost vizitat : viz[k]=0

#include<fstream.h>

#include<conio.h>

int a[20][20],n,m,viz[100],gasit;

void dfmr(int nod)

{

cout<<nod<<" ";

viz[nod]=1;

for(int k=1;k<=n;k++)

if(a[nod][k]==1&&viz[k]==0)

dfmr(k);

}

void main()

{int x,y,j;

fstream f;

clrscr();

f.open("graf.txt",ios::in);

if(f)

cout<<"ok!"<<endl;

else

cout<<"eroare la deschidere de fisier!";

f>>n>>m;

for(int i=1;i<=m;i++)

{f>>x>>y;

a[x][y]=1;}

cout<<endl<<"matricea de adiacente"<<endl;

for(i=1;i<=n;i++)

{for(j=1;j<=n;j++)

cout<<a[i][j]<<" ";

cout<<endl;}

cout<<endl<<"parcurgere in adancime incepand de la varful 1"<<endl;

dfmr(1);

getch();} 

Aplicatii :

1.Sa se parcurga graful in adancime pornind pe rand de la toate varfurile

2. Sa se determine daca pornind de la varful x se poate ajunge la varful y

3. Sa se determine daca se poate parcurge pornind de la un varf tot graful

Intr-un parc de distractii exista « Casa Labirint ». Aceasta este formata din n incaperi intre care se gasesc culoare cu un singur sens de parcurgere. Se stie stie incaperea de la care se porneste.

a) Sa se determine care sunt incaperile cu cele mai multe coridoare de legatura

b) Care sunt incaperile in care traseul se blocheaza (fara iesire)

c) Exista vreo incapere care sa aiba acces direct la toate celelalte