Parcurgerea
Rezolvarea
multor probleme de grafuri, presupune parcurgerea lor de la un anumit nod.
Pentru explorarea grafurilor, exista doua tipuri de algoritmi: de explorarea in
latime si de explorare in adancime. Parcurgerea grafurilor orientate este similara
cu a grafurilor neorientate, se tine cont insa de orientare.
Explorarea
grafurilor in latime
La
explorarea in latime, dupa vizitarea varfului initial, se exploreaza toate
varfurile adiacente lui, se trece apoi la primul varf adiacent si se exploreaza
toate varfurile adiacente acestuia si neparcurse inca, s.a.m.d.
Fiecare
varf se parcurge cel mult odata.
De
exemplul pentru garful din figura de mai jos, se va proceda in felul urmator:
se porneste din nodul 1, (se poate incepe de
la oricare alt nod)

se exploreaza in vontinuare
vecinii acestuia : nodul 2 si apoi 4,
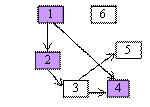 se obtine 1,2,4
se obtine 1,2,4
dupa care din 2 se exploreaza nodul adiacent
acestuia 3. Nodul 1 nu se mai viziteaza odata
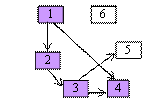 se obtine 1,2,4,3
se obtine 1,2,4,3
In continuare ar trebui parcursi vecinii lui 4
(1,2,4,3 ) dar acesta nu mai are vecini nevizitati si se
trece la vecinii lui 3 : 1,2,4,3 respectiv nodul 5 :
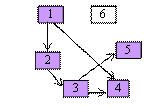 se obtine 1, 2, 4, 3,
5
se obtine 1, 2, 4, 3,
5
Varful 6 ramane neparcurs
Daca se parcurge graful
incepand de la varful 2, solutia este : 2,3,4,5, in timp ce
parcurgerea incepand cu 4 va retine doar varful 4
Algoritmul
Se va folosi o coada in care se inscriu nodurile in forma in care
sunt parcurse: nodul initial varf (de
la care se porneste), apoi varfurilr a,b,..., adiacente lui varf, apoi cele adiacente lui a, cele
adiacente lui b,... ,s.a.m.d.
Coada este folosita astfel:
- se incarca primul varf in coada;
- se afla toate varfurile adiacente cu primul nod si se introduc dupa primul
varf
- se ia urmatorul nod si i se afla nodurile adiacente
- procesul se repeta pana cand se ajunge la sfarsitul cozii
-Graful
se va memora utilizand matricea de adiacenta a[10][10]
-pentru
memorarea succesiunii varfurilor parcurse se va folosi un vector c[20] care va
functiona ca o coada
-pentru
a nu parcurge un varf de doua ori se va folosi un vector boolean viz[20] care
va retine :
-
viz[k]=0 daca varful k nu a fost vizitat inca
-
viz[k]=1 daca varful k a fost vizitat
-doua
variabile : prim si ultim vor retine doua pozitii din vectorul c si
anume :
-
prim este indicele componentei pentru care se parcurg vecinii (indexul
componentelor marcate cu rosu in sirurile parcurse anterior ). Prin urmare
Varf=c[prim], este elementul pentru care se determina vecinii (varfurile
adiacente)
-ultim
este pozitia in vector pe care se va face o noua inserare in vectorul c
(evident, de fiecare data cand se realizeaza o noua inserare se mareste
vectorul)
-vecinii
unui varf se « cauta » pe linia acestui varf : daca a[varf][k]=1
inseamna ca varf si k sunt adiacente.
Pentru ca varful k sa fie adaugat in coada trebuie ca varful sa nu fi fost
vizitat : viz[k]=0
#include<fstream.h>
#include<conio.h>
int
a[10][10],c[20],viz[10];
int
n,m,prim,ultim,varf;
void bf_iterativ() //parcurgerea in latime
{int k;
while(prim<=ultim)
{varf=c[prim];
for(k=1;k<=n;k++)
if(a[varf][k]==1&&viz[k]==0) //il adaug pe k in coada
daca este vecin pt. varf si nu a fost
vizitat
{ultim++;
c[ultim]=k;
viz[k]=1;}
prim++;
}
}
void main()
{clrscr();
int x,y;
fstream f; //memorare graf in matrice de adiacenta
f.open("muchii.txt",ios::in);
f>>n>>m;
for(int i=1;i<=m;i++)
{f>>x>>y;
a[x][y]=1;
}
cout<<"matricea
de adiac "<<endl; // afisare matrice de adiacenta
for( i=1;i<=n;i++)
{for(int j=1;j<=n;j++)
cout<<a[i][j]<<" ";
cout<<endl;
}
int nd;
prim=ultim=1;
cout<<"varful de inceput=";
cin>>nd;
//
varful de la care se porneste
parcurgerea
viz[nd]=1;
c[prim]=nd;
bf_iterativ();
for(i=1;i<=ultim;i++) //afisarea cozii
cout<<c[i]<<" ";
getch();
}
Varianta recursiva de parcurgere se obtine modificand functia de parcurgere iterativa adaugand conditia necesara autoapelului:
void bf_recursiv() //parcurgerea in latime
{int k;
if(prim<=ultim)
{varf=c[prim];
for(k=1;k<=n;k++)
if(a[varf][k]==1&&viz[k]==0) //il
adaug pe k in coada daca este
vecin pt. varf si nu a fost
vizitat
{ultim++;
c[ultim]=k;
viz[k]=1;}
prim++;
bf_recursiv();
}
}
Parcurgerea
in latime a grafurilor memorate prin liste
este similara cu diferenta cavecinii unui nod adaugat in coada se cauta in lista corespunzatoare lui :
#include<conio.h>
#include<fstream.h>
struct nod
{int
nd;
nod *next;};
nod *L[20];
int viz[100];
//marchez cu 1 nodurile vizitate
int m,n;
int
prim,ultim,C[100];
void bfi_lis()
{int varf,nr;
nod *p;
while(prim<=ultim)
{varf=C[prim];
p=L[varf]; // se parcurge lista elementelor din varful cozii
while(p)
{nr=p->nd;
if(viz[nr]==0) //numai daca nu
a fost vizitat
{ultim++;
//maresc coada
C[ultim]=nr; //il adaug
in coada
viz[nr]=1;}; //il marchez
ca fiind vizitat
p=p->next;
}
prim++; //avansez la urmatorul varf din coada
}
}
void afisare(int nr_nod)
{nod *p=L[nr_nod];
if(p==0)
cout<<nr_nod<<" este izolat "<<endl;
else
{cout<<"lista vecinilor lui
"<<nr_nod<<endl;
nod *c=p;
while(c)
{cout<<c->nd<<" ";
c=c->next;}
cout<<endl;}
}
void
main()
{fstream f;
int i,j;
nod *p,*q;
f.open("muchii.txt",ios::in);
clrscr();
f>>n>>m;
while(f>>i>>j)
{p=new nod;
p->nd=j;
p->next=L[i];
L[i]=p;
}
f.close();
cout<<endl<<"listele
de adiacente ";
for(i=1;i<=n;i++)
afisare(i);
int ndr;
cout<<endl<<"nodul
de inceput ";
cin>>ndr;
viz[ndr]=1;
prim=ultim=1;
C[prim]=ndr;
cout<<endl<<"parcurgere in latime
"<<endl;
bfi_lis();
for(i=1;i<=ultim;i++)
cout<<C[i]<<"
";
getch();
}
Functia recursiva :
void bfr_lis()
{int varf,nr;
nod *p;
if(prim<=ultim)
{varf=C[prim];
p=L[varf];// se parcurge lista elementelor din varful cozii
while(p)
{nr=p->nd;
if(viz[nr]==0)//numai daca nu
a fost vizitat
{ultim++;//maresc
coada
C[ultim]=nr;//il adaug
in coada
viz[nr]=1;};//il marchez ca fiind vizitat
p=p->next;}
prim++; //avansez la urmatorul nod din
coada
bfr_lis();
}
}
Aplicatii :
1.Sa se parcurga
graful in latime pornind pe rand de la toate varfurile
2. Sa se
determine daca pornind de la nodul x se poate ajunge la nodul y
3. Sa se
determine daca se poate parcurge pornind de la un nod tot graful