REPREZENTAREA GRAFURILOR
NEORIENTATE
Fie G=(V, E) un graf neorientat.
Exista mai multe modalitati de
reprezentare pentru un graf neorientat, folosind diverse tipuri de structuri de
date. Reprezentarile vor fi utilizate in diversi algoritmi si in programele
care implementeaza pe calculator acesti algoritmi.
Matricea de adiacentă matricea booleană
Matricea de adiacentă asociată unui graf
neorientat cu n noduri se defineste
astfel: A = (ai j) n
x n cu
![]() 1, daca [i,j]ÎE
1, daca [i,j]ÎE
a[i,j]=
0,
altfel
Observatii:
-
Matricea de adiacenta asociată unui graf neorientat este
o matrice simetrică
-
Suma elementelor de pe linia k reprezintă gradul nodului
k
-
Suma elementelor de pe coloana k reprezintă
gradul nodului k
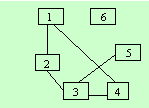
Fie graful din
figura urmatoare:
0 1
0 1 0
0 nodul 1 are gradul 2
1 0
1 0 0
0 nodul 2 are gradul 2
A= 0 1
0 1 1
0 nodul 3 are gradul 3
1 0
1 0 0
0 nodul 4 are gradul 2
0 0 1
0 0 0
nodul 5 are gradul 1
0 0 0
0 0 0
nodul 6 are gradul 0
Numarul de noduri este 6 si numarul de muchii este 5
Matricea este simetrica si patratica avand 6 linii si 6 coloane
Diagonala principala contine numai valori nule
Pentru a prelucra graful se citesc:
6- reprezentand n, numarul de noduri
5- reprezentand m, numarul de muchii
5 perechi x-y reprezentand extremitatile celor
5 muchii:
1-2 => a[1,2]=a[2,1]=1
1-4 => a[1,4]=a[4,1]=1
2-3 => a[2,3]=a[3,2]=1
3-4=>
a[3,4]=a[4,3]=1
3-5 => a[3,5]=a[5,3]=1
Probleme propuse:
Problema 1
Se citeste un
graf din fisierul graf.txt: numarul de noduri, numarul de muchii si muchiile.
a) sa se afiseze
matricea de adiacente
b) Sa se
determine gradul unui nod citit
c) Sa se afiseze
pentru un nod citit nodurile adiacente
d) sa se afiseze
nodurile incidente cu cea de a x muchie din matrice
e) sa se afiseze pentru
fiecare nod gradul
f) sa se afiseze
nodul (nodurile) avand cei mai multi vecini
g) sa se afiseze
nodurile izolate
h) sa se
determine daca o secventa de m noduri citite de la tastatura este un lant din
graf
Problema 2
Sa se det daca o
matrice citita dintr-un fisier poate fi matricea unui graf neorientat. In caz
afirmativ se va determina cate muchii are graful
Problema 3
Sa se genereze un
graf avand n noduri. Sa se afiseze matricea atasata
Observatie:
graful nu poate fi decat cel mult
complet
Problema 4
Sa se determine
daca un graf este regulat
Problema 5
In fisierele
g1.txt si g2.txt sunt memorate doua grafuri neorientate astfel: pe prima linie
o valoare naturala n reprezentand nodurile si apoi muchiile. Sa se determine
daca g2 este graf partial pentru g1.
Problema 6
In fisierul
g1.txt este memorat un graf neorientat. Se cunosc numarul de noduri si
muchiile. In fisierul g2.txt sunt memorate un nr x apoi cele x valori (ce ar putea reprezenta
nodurile ramase) iar la sfarsit perechi de valori. Sa se determine daca datele
din cel de al doilea fisier reprezinta un subgraf pentru primul graf.
Problema 7
Un graf neorientat este bipartit daca exista o partitie a multimii nodurilor in doua multimi A si B astfel incat oricare doua varfuri din aceeasi multime sa nu fie adiacente. Sa se scrie un program care verifica daca un graf este bipartit si in caz afirmativ sa se tipareasca multimile A si B
Problema 8
Sa se genereze toate grafurile cu n noduri si m muchii (n<=5)
Problema 9
Sa se genereze toate grafurile bipartite cu n noduri
Problema 10
Sa se determine daca un graf este hamiltonian. In caz afirmativ se va afisa un ciclu hamiltonian
Problema 11
Se considera un grup de n persoane. Pentru persoane se cunosc numele. Fiecare persoana are cel putin n/2 prieteni. Prietenii sunt dati ca perechi de nume. Una dintre persoane are o carte pe care fiecare doreste sa o citeasca. Sa se determine o modalitate prin care cartea sa circule pe la fiecare persoana exact o data, transmiterea ei facandu-se numai intre doi prieteni, iar in final cartea sa ajunga din nou la proprietarul cartii.
Problema 12
In tabara prieteniei au venit n copii. Se cunoaste numele celor n copii. Unii copii sunt prieteni deja si se urmareste sa se lege noi prietenii. Se cunosc cele m perechi de copii prieteni. In cea de a doua zi a taberei urmeaza sa se organizeze 2 excursii astfel incat in fiecare excursie sa fie inclusi numai copii care nu sunt deja prieteni. Sa se determine daca se pot imparti copii in doua astfel de grupe. In caz afirmativ se vor afisa cele doua grupe de copii.
Problema 13
Sa se determine daca un graf este complet
Problema 14
Scrieti un program care determina, pentru un graf dat cu n varfuri si un numar k, subgraful cu numar maxim de varfuri si cu proprietatea ca orice varf al sau are gradul cel putin k. Sau, daca un asemenea subgraf nu exista, sa se dea un mesaj corespunzator. Se vor afisa nodurile si muchiile ramase.
Problema 15
Problema colorarii unei harti. Se citesc 4 culori
(siruri de caractere) si denumirile a n tari (siruri de caractere) . Se cunosc
de asemeni tarile vecine. Sa se coloreze harta astfel incat sa nu existe doua
tari alaturate avand aceeasi culoare. Se
va afisa o solutie : tara-culoare, tare-culoare etc.
Ex :
6 tari
Ucraina,Romania,Ungaria,Moldova,Bulgaria,Serbia
9 vecinatati
Romania-Ungaria
Romania – Ucraina
Romania-Moldova
Romania-Bulgaria
Romania-Serbia_si_Muntenegru
Serbia_si_Muntenegru-Ungaria
Ungaria-Ucraina
Ucraina-Moldova
Bulgaria- Serbia_si_Muntenegru
Daca cele 4 culori sunt: rosu, galben, albastru, verde
O solutie este:
Romania –rosu
Ungaria-galben
Ucraina-albastru
Moldova –galben
Bulgaria-galben
Serbia –albastru
Problema 16
Sa se genereze, daca este posibil un graf cu n noduri cu grad cunoscut pentru fiecare nod. Daca nu este posibil se va afisa un mesaj.