REPREZENTAREA GRAFURILOR ORIENTATE

Fie G=(V, E) un graf orientat.

Exista mai multe modalitati de reprezentare pentru un graf orientat, folosind diverse tipuri de structuri de date. Reprezentarile vor fi utilizate in diversi algoritmi si in programele care implementeaza pe calculator acesti algoritmi.

Matricea de adiacentã matricea booleanã

Matricea de adiacentã asociatã unui graf orientat cu n noduri se defineste astfel: A = (a_{i j}) _{n x n} cu

1, daca [i,j]ÎE

a[i,j]=

0, altfel

Observatii:

- Matricea de adiacenta asociatã unui graf orientat nu este o matrice simetricã (doar daca pt fiecare arc (i,j) ar exista si arcul (j,i) asociat)

- Suma elementelor de pe linia k reprezintã gradul exterior al varfului k

- Suma elementelor de pe coloana k reprezintã gradul interior al varfului k

Fie graful din figura urmatoare:

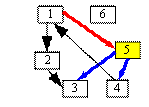
0 1 0 0 1 0

0 0 1 0 0 0

A= 0 0 0 0 0 0 Varful 5 are - gradul exterior 2 (vezi linia 5)

1 0 0 0 0 0 - gradul interior 1 (vezi coloana 5)

0 0 1 1 0 0

0 0 0 0 0 0

Observatie: numarul valorilor de 1 din matrice va fie gal cu numarul de arce.

Varful 6 are gradul interior 0, exterior 0 si este varf izolat

Pentru a prelucra graful se citesc:

6- reprezentand n, numarul de varfuri

6- reprezentand m, numarul de arce

6 perechi x-y reprezentand extremitatile celor 6 arce:

1-2 => a[1,2]=1

1-5 => a[1,5]=1

2-3 => a[2,3]=1

4-1=> a[4,1]=1

5-3 => a[5,3]=1

5-4 => a[5,4]=1

Problema :

Se citeste un graf din fisierul graf.txt: numarul de varfuri, numarul de arce si arcele.

a) sa se afiseze matricea de adiacente

b) Sa se determine gradul unui varf citit

c) sa se afiseze pentru fiecare varf gradul

d) sa se afiseze varful cu cel mai mare grad

e) sa se afiseze varfurile izolate

f) sa se determine daca o succesiune de varfuri citite reprezinta un drum din graf. In caz afirmativ se va determina daca drumul este elementar sau drumul este simplu

g)din fisierul graf2.txt se citeste alt graf. Sa se determine daca cel de al doilea graf este graf partial pentru primul