Divide et Impera. Aplicatii
Probleme:
1.
Se citeste un numar natural
n si n numere naturale. Sa se calculeze cel mai mare divizor comun al celor n
numere, folosind un algoritm Divide et Impera.
2.
Scrieti un program
pentru determinarea minimului dintr-un sir de numere intregi, folosind Divide
et Impera.
3.
Scrieti un program
pentru calculul sumei valorilor dintr-un sir de numere intregi, folosind Divide
et Impera.
4.
Sa se determine cate
elemente pare are un vector
5.
Fie un tablou
neordonat de numere intregi. Sa se determine prin metoda D&I de cate ori
apare in tablou o anumita valoare v.
6.
Implementati
algoritmul de cautare binara.
7.
Problema punctului
fix: Sa se gaseasca intr-un
vector cu n elemente un element cu proprietatea ca valoarea lui este egala cu
pozitia pe care apare. (a[k]=k)
8.
Fie un tablou
neordonat de numere intregi. Sa se determine prin metoda D&I toate
pozitiile in care apare in tablou o anumita valoare v.
9.
Fie un v vector de
numere intregi. Sa se determine valoarea expresiei:
a) v[1]+2v[2]2+3v[3]3+.....+nv[n]4
b) (1+v[1])(1+v[2])......(1+v[n-1])(1+v[n])
10. Se dau n numere intregi pentru care se cere sa se afiseze
modalitatea de calcul a produsului lor prin metoda D&I
Ex: pentru n=5 se va afisa ((x1*x2)*x3)*(x4*x5)
11. Scrieti o functie care inverseaza un sir de caractere,
folosind tehnica Divide Et Impera.
12. 
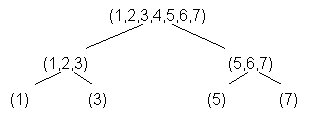Se considera un vector de lungime n. Definim plierea
vectorului prin suprapunerea celor doua jumatati. Daca n este impar, elementul din
mijloc se elimina. Jumatatile obtinute se pliaza la randul lor, pana cand se
ajunge la subvectori de lungime 1, numiti elemente finale. Sa se afiseze toate
elementele finale posibile.
Ex: n=7, a=(1,2,3,4,5,6,7), elementele finale vor fi 1, 3, 5, 7
13. Scrieti un program prin care calculatorul sa ghiceasca
din cat mai putine incercari un numar natural [1..10000] la care va ganditi in
prealabil. Atunci cand calculatorul propune un nr, ii raspundeti cu 1 daca nr
este prea mare, cu -1 daca e prea mic si cu 0 daca a ghicit
14. Se citesc numele si inaltimile a n persoane. Sa se
afiseze persoanele avand inaltimea mai mare sau egala cu un h citit. Sa se
ordoneze crescator persoanele dupa inaltime. Sa se afiseze o persoana avand o
inaltime data. Daca nu exista o astfel de persoana se va afisa un mesaj.
15. Sa se determine valoarea unui polinom intr-un punct
utilizand metoda Divide et Impera
16. Sa se determine suma o doua polinoame utilizand metoda
D&I
17. Se citesc lungimea si latimea unui dreptunghi. Dreptunghiul
se perpendicular pe latura mai mare in doua. Apoi dreptunghiul astfel obtinut
se taie in doua dupa latura mai mare si
asa mai departe. Sa se determine daca prin taieri succesive a dreptunghiurilor
astfel obtinute se poate ajunge la un patrat cu latura mai mare decat un
epsilon citit.
Ex L=10, l=1.25 , eps=0.1se obtine un patrat cu latura 1.25
18. Placa perforata. Se da o bucata dreptunghiulara de tabla cu lungimea L si inaltimea H,
avand pe suprafata ei n gauri de coordonate numere intregi (relativ la coltul
din stanga-jos al placii). Se cere sa se decupeze din placa o bucata de arie
maxima care nu prezinta gauri. Sunt permise numai taieturi orizontale si
verticale.
Se citesc numarul de perforatii, coordonatele relative la coltul stanga jos
al tablei al perforatiilor si lungimea si latimea tablei
Ex: pentru:
7
2 17
4 7
31 2
14 20
25 13
31 24
14 1
40 30
Se obtine:
Cea mai mare suprafata neperforata are coordonatele (4,1) ; (25,20)
Are suprafata 399
19. Sa se determine suma elementelor unei matrici utilizand
metoda D&I.
20. Se citesc numele a n persoane si inaltimile
a)
Sa se determine daca
persoanele sunt ordonate dupa inaltime
b)
Sa se afiseze
persoana cea mai inalta
c)
Care este inaltimea
medie?
d)
Sa se ordoneze
alfabetic persoanele prin metoada QuickSort
e)
Sa se afiseze inaltimea
unei persoane al carei nume se va citi de la tastatura (cautare binara dupa
nume)
f)
Sa se ordoneze
persoanele descrescator dupa inaltime utilizand MergeSort
g)
Sa se afiseze toate
persoanele cu inaltimea mai mare de 1.70
h)
Sa se determine cate
persoane au inaltimea 1.80
21.
n copii culeg mere . Sa se
determine:
a) copilul care a cules cele mai multe mere
b)copii care au cules mai mult de x mere si numarul lor
c)daca sunt copii care au cules acelasi
numar de mere
d)ordonati crescator copii dupa nr de mere culese folosind D et I
e)numarul de mere culese in total
22. Problema turnurilor din Hanoi.
23. Fie un vector cu n elemente. Se imparte vectorul in doua
parti. In jumatatea din stanga, elementele se vor micsora cu 1, iar elementele din
jumatatea dreapta se maresc cu 1. Daca vectorul are numar impar de elemente,
elementul din mijloc ramane nemodificat. Se repeta operatiunea cu jumatatile de
vector, pana cand se ajunge la portiuni de vector cu un singur element. Sa se
afiseze configuratia finala a vectorului.
Exemplu: n=11, a={1,2,3,4,5,6,7,8,9,10,11} à se va obtine a={-2,1,2,3,6,6,6,9,10,11,14}
24. Se da un vector cu n numere intregi. Se imparte tabloul
in 3 subgrupe, cat mai echilibrate ca dimensiune, eliminandu-se in fiecare grup
mijlocul sau mijloacele (pentru nr. par de elemente). Se repeta procedeul
pentru fiecare din cei 6 subvectori obtinuti. Procedeul se repeta de p ori. Sa
se afiseze vectorul obtinut dupa terminarea algoritmului.
Ex: n=50, x[i]=i, i=1,50, p=2 se va obtine:
5,7,14,16,19,21,22,24,28,30,31,33,36,38,39,41,45,48,50
25. Sa se sorteze un vector folosind algoritmul de sortare
rapida Quick-Sort.
26. Sa se ordoneze n puncte din plan utilizand QS dupa
distanta fata de origine.
27. Sa se sorteze un vector, folosind algoritmul de sortare
prin interclasare.
28. Se considera un patrat format din 2n x 2n patratele unitare. Fiecare patratel trebuie
codificat printr-un sir de n cifre din multimea {1,2,3,4}, astfel:
-
toate
codurile din patratul din stanga-sus (patrat cu latura egala cu jumatate din
latura patratului mare) au prima cifra egala cu 1; codurile din patratul din
dreapta-sus au prima cifra 2; cele din patratul din dreapta-jos au prima cifra
3 si cele din stanga-jos au prima cifra 4
-
oricare din
cele 4 patrate definite anterior poate fi impartit in 4 subpatrate, a doua
cifra a codurilor fixandu-se 1,2,3 sau 4, dupa cum subpatratul este situat in
stanga-sus, dreapta-sus, dreapta-jos sau stanga-jos
-
operatiunea
de divizare a subpatratelor in alte subpatrate se incheie cand s-a ajuns la un
patrat cu latura 1.
Realizati
un program care scrie in fisierul careu.txt, pe linii, codurile
corespunzatoare patratului de latura 2n, n citit de la tastatura.
Exemplu:
pentru n=4, patratul va arata astfel:
1111
1112 1121 1122 1211 1212 1221 1222 2111
2112 2121 2122 2211 2212 2221 2222
1113
1114 1123 1124 1213 1214 1223 1224 2113
2114 2123 2124 2213 2214 2223 2224
1131 1132 1141 1142 1231 1232 1241 1242 2131 2132 2141 2142 2231 2232 2241 2242
1133 1134 1143 1144 1233 1234 1243 1244 2133 2134 2143 2144 2233 2234 2243 2244
1311 1312 1321 1322 1411 1412 1421 1422 2311 2312 2321 2322 2411 2412 2421 2422
1313 1314 1323 1324 1413 1414 1423 1424 2313 2314 2323 2324 2413 2414 2423 2424
1331 1332 1341 1342 1431 1432 1441 1442 2331 2332 2341 2342 2431 2432 2441 2442
1333 1334 1343 1344 1433 1434 1443 1444 2333 2334 2343 2344 2433 2434 2443 2444
3111 3112 3121 3122 3211 3212 3221 3222 4111 4112 4121 4122 4211 4212 4221 4222
3113 3114 3123 3124 3213 3214 3223 3224 4113 4114 4123 4124 4213 4214 4223 4224
3131 3132 3141 3142 3231 3232 3241 3242 4131 4132 4141 4142 4231 4232 4241 4242
3133 3134 3143 3144 3233 3234 3243 3244 4133 4134 4143 4144 4233 4234 4243 4244
3311 3312 3321 3322 3411 3412 3421 3422 4311 4312 4321 4322 4411 4412
4421 4422
3313 3314 3323 3324 3413 3414 3423 3424 4313 4314 4323 4324 4413 4414
4423 4424
3331 3332 3341 3342 3431 3432 3441 3442 4331 4332 4341 4342 4431 4432
4441 4442
3333 3334 3343 3344 3433 3434 3443 3444 4333 4334 4343 4344 4433 4434
4443 4444