Grafuri neorientate. Probleme propuse

1. Fie un graf neorientat memorat prin matricea de adiacente si o succesiune de k noduri. Sa se determine daca succesiunea citita este un lant din graf
2. Din fisierele mat1.in si mat2.in se citesc doua matrici patratice associate grafurilor g1 si g2. Sa se deremine daca g2 este graf partial pentru g1
3. Fie o harta cu n orase. Cele n orase se citesc din fisier. Intre cele n orase exista m drumuri. Se cunosc distantele celor n drumuri.
1. Sa se determine daca orasul x si orasul y sunt vecine
2. Sa se afiseze lungimile tuturor localitatilor intre care exista drum direct
3. Sa se determine lungimea minima a drumului dintre doua localitati citite de la tastatura
4. La o receptie sunt invitate n personae. Se cunosc numele celor n persoane . Intre anumite persoane exista relatii de colaborare. Sa se determine daca se pot dispune cele n personae la o masa rotunda astfel incat intre oricare doua personae alaturate sa existe relatii. Se citesc : numele persoanelor si cele m relatiile sub forma de perechi de nume
5. Un eschimos locuieste la iglul cu numarul z. El are o harta pe care sunt marcate iglu-urile din zona (numerotate de la 1 la n) si distantele dintre acestea. Stiind ca din cauza frigului eschimosul nu poate sa parcurga o distanta mai mare de 20 km fara oprire, afisati o varianta de a ajunge la prietenul lui care locuieste la iglul cu numarul w, eventual cea mai scurta varianta care indeplineste cerinta data. Cati kilometri a parcurs eschimosul?
6. Un graf neorientat este bipartit daca exista o partitie a multimii nodurilor in doua multimi A si B astfel incat oricare doua varfuri din aceeasi multime sa nu fie adiacente. Sa se scrie un program care verifica daca un graf este bipartit si in caz afirmativ sa se tipareasca multimile A si B
7. Problema colorarii unei harti. Se citesc 4 culori (siruri de caractere) si denumirile a n tari (siruri de caractere) . Sa se coloreze harta astfel incat sa nu existe doua tari alaturate avand aceeasi culoare. Se va afisa o solutie : tara-culoare, tare-culoare etc.
8. Sa se coloreze un graf astfel incat oricare doua muchii incidente cu acelasi nod sa fie colorate diferit. Care este numarul minim de culori necesar.
9. O pestera are n incaperi, fiecare situata la o adancime h. Configuratia pesterii este data de cele m culoare de acces intre camerele pesterii (culoarele sunt date ca extremitati). In incaperea s exista un izvor de apa sulfuroasa. Se dau n, m, cele m culoare (ca perechi x-y), s si adancimile h ale camerelor. Determinati incaperile inundate si culoarele umezite.
10. Fie un graf neorientat. Sa se determine daca graful contine cicluri.
11. Fie un arbore (un graf neorientat conex şi fără cicluri) cu n vârfuri care conţine cel puţin două noduri terminale (frunze). Fiecare din cele n-1 muchii ale arborelui are asociat un cost (număr natural între 1 şi 2000). Definim costul arborelui ca fiind suma costurilor muchiilor arborelui.

Fiind dat un număr natural p, să se adauge o muchie de cost p între două noduri terminale i şi j din arbore şi apoi să se elimine o altă muchie din arborele iniţial, astfel încât să se obţină tot un arbore, iar diferenţa în modul dintre costul arborelui iniţial şi costul noului arbore să fie minimă.

Date de intrare

Fişierul arbore.in conţine pe prima linie valorile lui n şi p (p reprezentând costul muchiei care se va adăuga în arbore), iar pe următoarele n-1 linii câte trei numere i, j, c, separate prin câte un spaţiu, cu semnificaţia: nodurile i şi j sunt adiacente în arbore, iar muchia [i,j] are costul c.

Date de ieşire

Fişierul arbore.out conţine pe prima linie trei numere întregi i, j şi c, separate prin câte un spaţiu, i şi j reprezentând extremităţile muchiei care se elimină şi c costul acesteia. Pe a doua linie se află două numere întregi x, y reprezentând cele două noduri terminale care se vor unifica printr-o muchie de cost p. Pe ultima linie se află un singur număr D ce reprezintă diferenţa minimă dintre costul arborelui iniţial şi costul noului arbore.

Dacă sunt mai multe muchii care pot fi eliminate, se va elimina prima în ordinea apariţiilor în fişierul arbore.in.

Dacă se poate adăuga muchie între mai multe perechi de noduri terminale din arborele iniţial, se va alege acea muchie pentru care suma valorilor extremităţilor este minimă.

La afişarea muchiilor, se va afişa întâi extremitatea de valoare mai mică.

Exemplu

arbore.in	arbore.out	Explicaţie
7 7 2 4 1 2 5 1 1 2 4 1 3 2 3 6 4 3 7 3	1 2 4 4 6 3	S-a eliminat muchia [1,2] de cost 4, s-a adăugat muchia [4,6], bineînţeles de cost p=7, iar diferenţa în modul dintre costurile arborelui iniţial şi cel final este 3. Se mai putea elimina şi muchia [3,6], dar [1,2] apare înaintea ei în fişierul arbore.in Se mai puteau adăuga şi muchiile [5,6], [5,7], [4,7] dar suma 4+6 este mai mică decât 5+6, 5+7 sau 4+7

Statii

Infamul Overmind al zergilor a fost distrus si locul de origine al protossilor din Shakuras sta acum in ruine si fumegand. Ca Executor si comandant al fortelor Protoss ramase tu trebuie acum sa reunesti populatia neputinciosa de protossi si sa ii salvezi de zergi care inca ocupa cu nepasare pamanturile din Shakuras.Obiectivul tau este de a prelua controlul unei baze principale a civilizatiei Tassadariana si va trebui sa te folosesti de statiile de emisie receptie pentru ca doar acestea iti pot indica baza principala. Exista perechi de statii de emisie-receptie care emit si receptioneaza in mod direct semnale. Intre doua perechi de statii x si y care comunica direct timpul de emisie este t . Semnalele la doua statii pot ajunge fie direct fie indirect prin intermediul altor statii. Evident, pot exista statii situate in baze diferite care nu vor putea comunica semnale. Statiile care nu emit si nu primesc semnale sunt lipsite de importanta strategica. Vei putea determina o baza principala stiind ca in Ziua Q toate statiile vor incepe sa emita astfel incat fiecare statie va transmite un mesaj tuturor celorlalte statii din interiorul bazei in care se afla (doua statii se gasesc in interiorul aceleiasi baze daca sunt capabile sa-si transmita informatii direct sau indirect). Semnalele intre doua statii vor fi transmise pe traseele de comunicatie care necesita cel mai putin timp si se vor transmite in ambele sensuri. Datorita bruiajului nu se vor emite concomitent mai multe semnale in interiorul aceleiasi baze ci in mod succesiv astfel incat pentru a-si comunica informatii oricare doua statii dintr-o baza se va consuma o perioada de timp T. O baza principala va fi indicata de o valoare minima a lui T. Va trebui sa gasesti aceasta valoare.

Date de intrare

Fisierul statii.in contine un numar natural n reprezentand numarul de statii de emisie-receptie. In continoare, pe linii diferite se vor gasi triplete de numere naturale reprezentand perechile de statii x si y si timpul t de emisie de la x la y sau de la y la x

Date de iesire

In fisierul statii.out se va scrie numarul cerut reprezentand valoarea minima a lui T. Daca nu exista un astfel de numar se va scrie 0.

Restrictii si precizari

1<=n<=100 numar natural

1<=t<=3000 numar natural

Numarul de baze poate fi cel putin 1 si cel mult n.

statii.in	statii.out
8 1 2 10 1 3 5 2 4 20 3 4 3 1 4 2 2 3 4 5 6 1 6 7 2 7 8 4 6 8 1 7 5 3	24

Timp de executie 1s/test

12. Fiind date mxn camere dispuse sub forma unei matrici astfel incat intre oricare doua camere alaturate se poate circula daca ambele retin 0. Sa se treaca matricea intr-un graf (camerele retin 0 cu semnificatia ca pot fi parcurse).

Ex:

Pt m=2 si n=4

1	0	1	0
1	1	0	1

Vom numerota camerele de la 1 la mxn

Se obtine:

1	2	3	4
5	6	7	8

Ceea ce inseamna ca se poate circula de la 2 la 7 (si invers) si de la 4 la 7 (si invers)

Se va asocia fiecarei componente a[i][j] un nod avand valoarea x=(i-1)*n +j.

Se obtine graful :

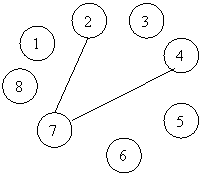
Matricea b asociata va fi o matrice avand (mxn) x (mxn) componente pentru care b[2][7]=b[7][2]=1 si b[7][4]=b[4][7]=1

Operatia inversa (de reconstruire a matricii pornind de la graf ) este determinata de :

i=(x-1)/nc +1

j=(x-1)%nc+1

13. Dintr-un fisier se citesc datele unui labirint cu mxn incaperi. Camerele retin 0 si 1. Se poate trece dintr-o camera in alta daca sunt alaturate si ambele retin 0. Sa se determine drumul cel mai scurt intre doua incaperi. Datele se citesc din fisier.
14. Aceeasi problema ca la pb 13 cu diferenta ca se considera ca doua persoane pornesc una catre cealalte din doua pozitii date astfel incat la un moment dat o persoana poate intra intr-o camera alaturata sau poate ramane pe loc.
15. pe o tabla de sah de dimensiuni nxn se poate deplasa un nebun conform regulilor sahului. In plus, pe tabla de sah sunt amplasate diverse obstacole la diferite coordonate. Sa se determine daca nebunul se poate deplasa intre x1 ,y1 si x2, y2 si, in caz afirmativ, sa se tipareasca numarul minim de mutari
16. Aceeaisi problema pentru un cal
17. Aceeasi problema pentru o regina