Recursivitate. Probleme
propuse
Probleme:
1.
Sa se srie
o functie recursiva care afiseaza
valorile de la 1 la n
2.
Sa se scrie o functie recursiva care afiseaza
valorile de la n la 1
3.
Sa se scrie o functie recursiva care calculeaza
n!
4.
Sa se scrie o functie
recursiva care calculeaza suma primelor n numere naturale
5.
Sa se scrie o functie recursiva care calculeaza
produsul a*b (ca fiind o adunare repetata)
6.
Sa se scrie o functie recursiva care calculeaza
ab
7.
Sa se scrie o functie recursiva care calculeaza
a: b (ca fiind o scadere repetata ) Ex: 11: 2 =5 rest
1
8.
Sa se descompuna
un numar in suma de doua numere:
Ex 11 se descompune in: 1+10, 2+9,
3+8, 4+7, 5+6
9. Expresii:
1*2+2*3+3*4+4*5
1+3+5+7+
1*4*7*10*
2*4*6*8* .
1x2+2x3+3x4+....+nx(n+1)
½+2/3+3/4+......+n/(n+1)
(1+2)x(2+3)x(3+4).....x(n+n+1)
10. Sa se determine :
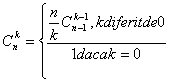
11.
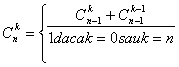
12.
Se citeşte x ξntreg. Se cere
programul pentru calculul funcţiei 9functia lui Manna
Pnueli):
![]()
13.
Se dă funcţia, definită pe
![]() . Se citesc m şi n. Să se calculeze Ack(m,n). Functia lui Ackerman
. Se citesc m şi n. Să se calculeze Ack(m,n). Functia lui Ackerman
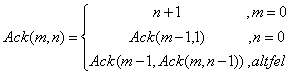
14.
Şirul lui Fibonacci. Se consideră şirul definit astfel:
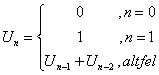
0,1,1,2,3,5,8,13
u(7)=13
15.
Se dau două numere
naturale a şi b. Se cere să se calculeze cel mai mare divizor comun
al lor. Indicaţie: se foloseşte formula recursivă a celui mai
mare divizor comun
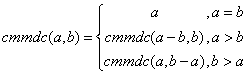
16.
Să se scrie o
funcţie recursivă care afiseaza cifrele
unui numar incepand de la unitati
N=1234
17.
Să se scrie o funcţie
recursivă pentru calculul sumei cifrelor unui număr natural.
18.
Să se scrie o funcţie
recursivă pentru transformarea unui număr natural n, din baza 10 ξn
baza k (1<k<10).
19.
Se consideră şirurile definite
recurent astfel: ![]()
![]()
Să se scrie un program care să citească a, b şi n şi
să calculeze ![]() şi
şi ![]() .
.
20.
Sa se calculeze, folosind o functie recursiva, valoarea expresiei ![]()
21. Sa se afiseze cifrele unui numar incepand de la unitati
22. Sa se determine suma cifrelor unui numar
23. Sa determine cifra cea mai mare a unui numar
24. sa se determine suma cifrelor pare ale unui numar
25. sa se numere cifrele unui numar
26. sa se numere cifrele pare ale unui numar
27. sa se numere de cate ori se gaseste
cifra x intr-un numar
28. sa se afiseze divizorii unui numar
29. Sa se numere divizorii unui numar
30. sa se determine suma divizorilor unui numar
31. Sa se determine daca un numar este
prim
32. inversul unui numar
33. Sa se genereze primii n termeni ai unei progresii aritmetice (geometrice), daca se cunosc primul termen si ratia.
34. un subprogram recursiv care determina de cate ori se gaseste o cifra intr-un numar
35. un subprogram recursiv care elimina spatiile dintr-un sir
36. un subprogram recursiv care elimina spatiile inutile dintr-un sir (intre subsiruri va ramane numai cate un spatiu)
37.
38.
Scrieti un subprogram
recursiv pentru determinarea si afisarea valorilor
din triunghiul lui Pascal pana la nivelul k. Amintim ca triunghiul lui Pascal
este format din coeficientii binomului lui Newton
(a+b)n, pentru n=1,2
k
Exemplu: pentru k=5, triunghiul este:
1
1 1
1
2 1
1
3 3 1
1 4
6 4 1
39. sa se afiseze o piramida de tipul:
1
2 2
3 3 3
4 4 4 4 etc
40.
Pentru n dat, sa se construiasca
recursiv triunghiul de numere de mai jos, fara a
folosi nici o instructiune repetitiva.
1
1 2
..
1 2
3
.. n-1
1 2
3
.. n-1 n
41.
Pentru n dat, sa se construiasca
recursiv triunghiul de numere de mai jos, fara a
folosi nici o instructiune repetitiva.
1 2
3
.. n-1 n
1 2
3
.. n-1
..
1 2
1
1.
Pentru n dat, sa se construiasca
recursiv triunghiul de numere de mai jos, fara a
folosi nici o instructiune repetitiva.
n n-1
n-2
..3 2 1
n n-1
n-2
..3 2
..
n n-1
n
2. un subprogram recursiv care determina daca o valoare se gaseste intr-un vector
3. citirea, afisarea unui vector recursiv
4. suma elementelor unui vector
5. suma elementelor pare dintr-un vector
6. Sa se calculeze, recursiv, maximul elementelor dintr-un vector
7. Scrieti o functie recursiva care afiseaza elementele unui vector in ordine inversa.
8. Se da un vector x cu n componente numere naturale cu cel mult 9 cifre. Sa se afiseze suma cifrelor componentelor vectorului.
9. un subprogram recursiv care calculeaza valoarea unui polinom de grad n intr-o valoare data
10. suma elementelor de pe o linie a unei matrici
11. suma elementelor de pe o coloana a unei matrici
12. afisarea elementelor de pe diagonalele pp si sec dintr-o matrice patratica
13. *un cioban isi cumpara oi. stiind ca o oaie dupa un an face o mieluta si mieluta devine dupa un an mioara iar mioara devine dupa un an oaie, ce va contine turma ciobanului dupa n ani?
Obs. Nu se nasc berbecuti si nici nu mor animale
dupa un an:
1 oaie si o mileluta nici o mioara
dupa doi ani:
o oaie, o mieluta si o mioara
dupa 3 ani:
2 oi,1 mioara , mielut 1
dupa 4 ani
3 oi, 1 mioara, 2 mieluti
14.
15.
Scrieti
o functie recursiva care transforma un numar din baza 10 in baza b (b<10).
16.
Scrieti
o functie recursiva care transforma un numar din baza b in baza 10 (b<10).
17.
O persoana are de coborat
n trepte. La fiecare pas, el poate cobori 1 sau 2 trepte. Cate posibilitati are de a cobori scara?
Exemplu: pentru n=12, exista 233 de posibilitati.
18.
Sa se descompuna
un numar in factori primi, folosind un algoritm
recursiv. (Ex: 19344=24*3*13*31)
19.
Numarul
de partitii ale unei multimi
cu n elemente in k submultimi este S(n,k), numit numarul lui Stirling de speta a II-a si este definit de relatiile:
S(n,1)=S(n,n)=1
S(n+1,k)=S(n,k-1)+kS(n,k)
Sa se calculeze numarul partitiilor
unei multimi cu n elemente in submultimi
de k elemente. Exemplu: S(5,3)=25
(Retineti acest
rezultat!)
20.
Se da un vector cu n elemente intregi. Sa se verifice, folosind o functie
recursiva, daca exista macar un element pozitiv in
vector.
21.
Fie sirul
1,2,2,3,3,3,
Gasiti o definitie
recursiva a acestui sir si scrieti un program care o implementeaza.
22.
Se considera ca diagonalele unei matrice patratice o impart pe aceasta in
4 zone: nord, sud, est si vest. Scrieti cate o functie recursiva pentru a calcula:
a.
Suma elementelor din nord
b.
Produsul elementelor din vest
c.
Numarul
de elemente pare din sud
d.
Procentul de zerouri din est
23.
Scrieti
un program care descompune un numar dat n ca suma de
puteri distincte ale lui 2.
Indicatie: Se va folosi o functie
care determina cea mai mare valoare p cu proprietatea ca 2p<=n
Exemplu: n=4978 se obtine descompunerea 21+24+25+26+28+29+212
24.
Sa se completeze in spirala, folosind un
algoritm recursiv, o matrice cu n linii si n coloane, cu primele n2
numere intregi.
Exemplu: pentru n=4
1 2
3 4
12 13 14 5
11 16 15 6
10 9
8 7
25.
Din numarul 4
se poate obtine orice numar
natural N scris in baza 10 prin aplicarea urmatoarelor
operatii:
a.
Se scrie la sfarsit
cifra 4
b.
Se adauga la sfarsit cifra 0
c.
Daca numarul
este par, se imparte la 2
Sa se scrie un program care produce un sir de
numere construit conform regulilor precedente, sir in care primul numar este 4 iar ultimul este N.
Exemplu: pentru N=7024, secventa este: 4 ΰ
2 ΰ
1 ΰ
14 ΰ
140 ΰ
1404 ΰ
702 ΰ7024.
Indicatie: Sirul se va genera
invers, de la N la 4, aplicand transformarile
inverse.
26.
Fie sirul
1,2,3,4,5,10,20,40,80,
ai carui termeni, incepand cu al saselea, satisfac relatia a[i]=a[i-1]*2. Sa se scrie un algoritm recursiv
care descompune un numar pozitiv n ca suma de termeni
distincti din sirul
definit.
Exemplu: pentru n=4578 se obtine descompunerea
3+5+10+80+640+1280+2560
27.
Codul Fibonacci
de ordinul n, n>=2, este secventa cn. Daca l
este sirul nul, atunci codul Fobonacci
se poate obtine recursiv astfel:
c2=(l),
c3=(0,1), c4=(00,01,10)
iar cn, n>4 se obtine
prin concatenarea a doua subsecvente: prima secventa
se obtine prefixand cu 0
fiecare codificare din cn-1, a doua prefixand
cu 10 fiecare codificare din cn-2. Elaborati
un algoritm care construieste codul lui Fibonacci pentru orice n dat.
Exemplu:
c5=(000,001,010,100,101)
28.
Sa se verifice daca doua matrici sunt identice, folosind o functie
recursiva.
29.
Afisati
tabla inmultirii cu x, folosind o functie
recursiva.
30.
Sa se afiseze, fara a utiliza instructiuni
repetitive, triunghiul:
2 4
6 ... 2(n-1) 2n
4 6
... 2(n-1) 2n
6 ... 2(n-1) 2n
.......
2(n-1) 2n
2n
Fractali
Fractalii sunt figuri geometrice care se repeta
in ele insele de un anumit numar de ori.
31.
Se deseneaza un
patrat cu latrura de o anumita
lungime. In exteriorul lui se deseneaza alte patrate cu latura egala cu jumatate
din latura patratului initial.
Se repeta procedeul de n ori (sau pana cand se obtin patrate cu latura suficient
de mica) cu fiecare din patratele obtinute.
Figura obtinuta se numeste
scara diavoluiui.

32.
Se deseneaza un
patrat cu latura de o anumita lungime. Se imparte patratul in 9 patrate egale si se hasureaza patratul din mijloc. Se repeta procedeul cu fiecare din
cele 8 patrate nehasurate
de la fiecare pas, pana se obtin patrate
cu o latura nesemnificativa. Figura obtinuta se numeste covorul lui Sierpinski.


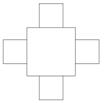
33.
Sa se scrie un program care deseneaza in mijlocul ecranului un patrat
cu latura L. In fiecare din varfurile patratului se deseneaza cate un patrat cu latura L/2. Se repeta procedeul pentru fiecare
din aceste patrate, sau de un anumit numar de ori, sau pana se obtin patrate cu latura nesemnificativa.
34.
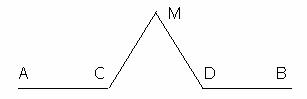
Linia de coasta Koch.
Fie un segment de drapta AB
dat prin coordonatele capetelor sale. Se imparte
segmentul in 3 segmente egale prin punctele C si D. Se construieste
triunghiul echilateral cu latura CD. Se sterge apoi
segmentul CD. Se procedeaza cu segmentele AC, CM, MD
si DB exact la fel cum s-a procedat cu AB. Se repeta procedeul de un anumit numar de ori.
35.
Sa se deseneze curba lui Koch pentru toate cele 3 laturi ale unui triunghi
echilateral, obtinandu-se astfel curba fulgului
de zapada.
36.
Sa se deseneze un patrat
cu diagonalele paralele cu axele de coordonate. Sa se deseneze patratul obtinut prin unirea
mijloacelor laturilor patratului initial.
Sa se repete procedeul cu fiecare patrat nou obtinut. Fiecare patrat va fi hasurat cu o culoare generata aleator.