Arbori de cautare
Se numeste arbore de cautare un arbore binar ale carui noduri au o cheie de identificare, iar pentru fiecare nod sunt valabile proprietatile urmatoare:
- Orice cheie asociata unui nod este mai mare decat cheia subordonatului stang
- Orice cheie asociata unui nod este mai mica decat cheia subordonatului drept
Cheile de
identificare sunt distincte.
Fie arborele din figura urmatoare. Cheile sunt : 30, 21 , 27, 15, 37, 31, 33, 36, 35, 24
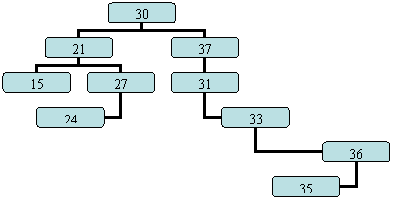
Observatie: ordinea de inserare a cheilor poate determina o alta configuratie pentru arbore. Spre exemplu daca se insereaza mai intai 30 si apoi 27 si 21 atunci 27 va deveni subordonat stang pentru 30 si 21 subordonat stang pentru 27.
Crearea arborilor de cautare se realizeaza aplicand de un numar de ori operatia de inserare. Inserarea se realizeaza astfel:
-se compara valoarea k de inserat cu cheia asociata nodului curent. Exista urmatoarele posibilitati:
- cheia coincide cu valoarea de inserat si se renunta la inserare
- cheia este mai mica decat k caz in care se incearca inserarea in subarborele drept
- cheia este mai mare decat k caz in care se incearca inserarea in subarborele stang
- inserarea propriuzisa se realizeaza atunci candsubarborele stang , respectiv drept, este vid, altfel se reia.
Parcurgerea arborilor de cautare se face ca orice arbore binar (svd, vsd sdv).
Cautarea unei valori se determina in mod similar cu subprogramul de inserare.
#include<iostream.h>
#include<conio.h>
struct nod
{int nr_o;
nod*st,*dr;
};
nod *v;
int n,k;
void inserare(nod *&c,int k)
{if(c)
if(c->nr_o==k)
cout<<"nr deja inserat "<<endl;
else
if(c->nr_o<k)
inserare(c->dr,k);
else
inserare(c->st,k);
else
{c=new nod;
c->nr_o=k;
c->st=c->dr=0;}
}
void svd(nod *c) //parcurgere in inordine
{if(c)
{svd(c->st);
cout<<c->nr_o<<" ";
svd(c->dr);
}
}
int cautare(nod *c,int k)
{if(c)
if(c->nr_o==k)
return 1;
else
if(c->nr_o<k)
cautare(c->dr,k);
else
cautare(c->st,k);
else
return 0;
}
void main()
{//v=0;
cout<<"nr de noduri ";
cin>>n;
for(int i=1;i<=n;i++)
{cout<<"valoarea de inserat ";
cin>>k;
inserare(v,k);}
cout<<endl<<"arborele are urmatoarele noduri "<<endl;
svd(v);
cout<<endl<<"valoarea de cautat ";
cin>>k;
if(cautare(v,k))
cout<<"s-a gasit!";
else
cout<<"nu s-a gasit!";
getch();
}
Probleme propuse
1. Litere
Se citeste un cuvant de la tastatura. Sa se genereze un arbore de cautare cu literele cuvantului.
a) sa se percurge svd, vsd, sdv arborele
b) sa se afiseze care vocale se gasesc si care nu se gasesc in arbore
c) sa se determine suma codurilor ascii a caracterelor din arbore
d) sa se afiseze frunzele arborelui
e) sa se determine suma codurilor ascii a caracterelor de pe nivelul x si nivelul cu cea mai mare suma
f) sa se determine daca doua caractere sunt „frati”
2. 6 din 49
Sa se genereze 40 de numere aleatoare cu valori cuprinse intre 1 si 49. Sa se afiseze 6 dintre ele.
3. Persoane
Sa se memoreze numele si prenumele a n persoane.
a) Sa se determine daca numele unei persoane a fost memorata in arbore.
b) Sa se afiseze persoanele ordonate alfabetic .
c) Sa se afiseze persoanele cu prenumele Dan
4. A fi sau a nu fi
Sa se determine daca un arbore binar este arbore de cautare sau nu
5. Sa se determine daca doi arbori binari de cautare sunt identici sau nu
6. Sa se construiasca un ABC inseilat (fiecare varf sa aiba legatura si catre predecesorul sau).
Pentru un nod avand o cheie data sa se afiseze:
a) predecesorul si succesorii
b) fratele
c) sa se verifice daca x si y sunt frati
7. Scrieti o functie care transforma un ABC intr-un ABC inseilat
8. Sa se stearga un nod intr-un ABC
9. Sa se inlocuiasca o cheie intr-un ABC
10. Sa se memoreze intr-un ABC numere intregi. Pt ca numerele se pot repeta se va retine frecventa de aparitie a acesora. Sa se afiseze numerele crescator.
11. Fie un ABC. Sa se afiseze pt fiecare nod valoarea asociata si apoi valorile subarborilor stang si drept intre paranteze separate prin virgula. Absenta unuia dintre subarbori va fi marcata cu *.

30(21(15,27(24,*)),37(31(*,33(*,36(35,*))),*))
12. Sa se determine minimul
(maximul ) dintr-un abc fara a parcurge tot arborele