Componente conexe

Fie G=(V, E) un graf neorientat, unde V are n elemente (n noduri) si E are m elemente (m muchii).

Definitie: G₁=(V₁, E₁)este o componenta conexa daca:

- pentru orice pereche x,y de noduri din V₁ exista un lant de la x la y (implicit si de la y la x)

- nu exista alt subgraf al lui G, G₂=(V₂, E₂) care sa indeplineasca prima conditie si care sa-l contina pe G₁

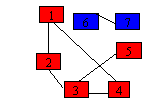
Graful alaturat are doua componente conexe: - subgraful care contine nodurile: 1 2 3 4 5 - subgraful care contine nodurile: 6 7

Observatie: subgraful 1, 2, 3, 4 nu este componenta conexa pentru ( chiar daca pentru orice pereche x,y de noduri exista un lant de la x la y) deoarece exista subgraful 1, 2, 3, 4, 5 care il contine si indeplineste aceeasi conditie.

Definitie: Un graf G=(V, E)este conex daca pentru orice pereche x,y de noduri din V exista un lant de la x la y (implicit si de la y la x).

Observatii:

- Un graf este conex daca admite o singura componenta conexa.

- Graful anterior nu este conex pentru ca admite doua componente conexe

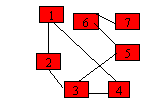
Graful urmator este conex:

Probleme:

1. Fiind dat un graf memorat prin intermediul matricei de adiacenta sa se determine daca graful este conex.

2. Fiind dat un graf memorat prin intermediul matricei de adiacenta si un nod k sa se determine componenta conexa careia ii apartine nodul k

3. Sa se afiseze toate componentele conexe ale unui graf neorientat

Indicatii :

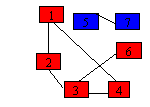
-In vectorul viz se incarca numarul componentei conexe astfel pentru graful urmator, vectorul viz va retine:

viz=[1,1,1,1,2,1,2].

-Numarul de componente conexe este 2.

-Se afiseaza componentele cu numarul componentei conexe egal cu 1: 1,2,3,4,6

-Se afiseaza componentele cu numarul componentei conexe egal cu 2: 5, 7

-Incarcarea in viz se realizeaza prin parcurgere df pornind de la fiecare nod

-se porneste de la 1, se parcurge df si se incarca in viz valoarea 1 pt nodurile 1, 2, 3, 4, 6. Viz devine:

1,1,1,1,0,1,0

-se porneste in continuare de la primul nod nevizitat, adica 5 si se incarca numarul celei de a doa componente, adica 2

Viz devine: 1,1,1,1,2,1,2

-Nu mai sunt noduri nevizitate si algoritmul se incheie.

Iata o solutie:

#include<fstream.h>

#include<conio.h>

int a[20][20],n,m,viz[100],gasit;

int nrc; //pastreaza numarul componentei conexe

void dfmr(int nod)

{ viz[nod]=nrc; //se incarca numarul componentei

for(int k=1;k<=n;k++)

if(a[nod][k]==1&&viz[k]==0)

dfmr(k);

}

void main()

{int x,y,j;

fstream f;

clrscr();

f.open("muchii.txt",ios::in); //memorare matrice de adiacenta

if(f)

cout<<"ok!"<<endl;

else

cout<<"eroare la deschidere de fisier!";

f>>n>>m;

for(int i=1;i<=m;i++)

{f>>x>>y;

a[x][y]=a[y][x]=1;}

cout<<endl<<"matricea de adiacente"<<endl;

for(i=1;i<=n;i++)

{for(j=1;j<=n;j++)

cout<<a[i][j]<<" ";

cout<<endl;}

for(int nod=1;nod<=n;nod++)

if(viz[nod]==0) //se incearca parcurgerea numai daca un nod nu a fost deja parcurs

{nrc++;

dfmr(nod);}

cout<<endl<<"vectorul viz "<<endl;

for(i=1;i<=n;i++)

cout<<viz[i]<<" ";

cout<<endl<<"Componentele conexe :"<<endl;

for(i=1;i<=nrc;i++)

{cout<<endl<<"componenta "<<i<<endl;

for(j=1;j<=n;j++)

if(viz[j]==i)

cout<<j<<" ";

}

getch();}

Probleme propuse:

1. Fie un graf conex. Sa se genereze un subgraf cu x noduri care sa fie tot conex
2. fie un graf cu n noduri. Sa se determine daca graful este conex, in caz contrar se va adauga un numar minim de muchii astfel incat graful sa devina conex