Componente tare conexe

Fie G=(V, E) un graf orientat, unde V are n elemente (n varfuri) si E are m elemente (m arce).

Definitie: G₁=(V₁, E₁)este o componenta tare conexa daca:

- pentru orice pereche x,y de varfuri din V₁ exista un drum de la x la y si drum de la y la x

- nu exista alt subgraf al lui G, G₂=(V₂, E₂) care sa indeplineasca prima conditie si care sa-l contina pe G₁

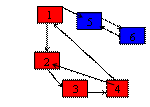
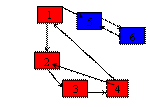
Graful alaturat are doua componente tare conexe: - subgraful care contine varfurile: 1 2 3 4 - subgraful care contine varfurile: 5 6

Observatie: subgraful 2, 3, 4 nu este componenta tare conexa ( chiar daca pentru orice pereche x,y de varfuri exista un drum de la x la y si de la y la x) deoarece exista subgraful 1, 2, 3, 4, care il contine si indeplineste aceeasi conditie.

Definitie: Un graf G=(V, E)este tare conex daca pentru orice pereche x,y de varfuri din V exista drum de la x la y si de la y la x.

Observatii:

- Un graf este tare conex daca admite o singura componenta tare conexa.

- Graful anterior nu tare este conex pentru ca admite doua componente tare conexe

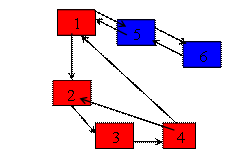
Graful urmator este tare conex:

Probleme:

1. Fiind dat un graf memorat prin intermediul matricei de adiacenta si un varf k sa se determine componenta conexa careia ii apartine varful k

2. Sa se afiseze toate componentele tare conexe ale unui graf neorientat

3. Fiind dat un graf memorat prin intermediul matricei de adiacenta sa se determine daca graful este tare conex.

Indicatii :

Pentru a determina componenta tare conexa careia ii apartine un varf x se determina succesorii acestuia (varfurile la care se poate ajunge pornind de la varful x) si in continuare se determina predecesorii acestuia (varfurile de la care pornind se ajunge la x). Se utilizeaza doi vectori : suc si prec pentru predecesori si succesori in care se va incarca x pentru nodurile parcurse. Pentru determinarea succesorilor si predecesorilor se utilizeaza parcurgerea in adancime astfel incat un successor pentru un varf k se gaseste pe linia k iar un predecessor pentru un varf k se gaseste pe coloana k.

Pentru graful din figura urmatoare daca se doreste determinarea componentei tare conexe careia ii apartine varful 4 :

cei doi vectori vor fi :

Vectorul suc :

4

4

4

4

4

4

4

Observatie : de la 4 pornind in adancime se pot parcurge toate varfurile

Vectorul prec :

4

4

4

4

4

0

0

Intersectia celor doi vectori reprezinta componenta tare conexa careia ii apartine varful 4.

Iata o modalitate de rezolvare :

//sa se determine componente tare conexa careia ii apartine un varf

#include<fstream.h>

#include<conio.h>

int a[20][20],n,m,suc[100],prec[100],x;

void dfsuc(int nod)

{suc[nod]=x;

for(int k=1;k<=n;k++)

if(a[nod][k]==1&&suc[k]==0)

dfsuc(k);

}

void dfprec(int nod)

{ prec[nod]=x;

for(int k=1;k<=n;k++)

if(a[k][nod]==1&&prec[k]==0)

dfprec(k);

}

void main()

{int y,j;

fstream f;

clrscr();

f.open("tare.in",ios::in);

if(f)

cout<<"ok!"<<endl;

else

cout<<"eroare la deschidere de fisier!";

f>>n>>m;

for(int i=1;i<=m;i++)

{f>>x>>y;

a[x][y]=1;}

cout<<endl<<"matricea de adiacente"<<endl;

for(i=1;i<=n;i++)

{for(j=1;j<=n;j++)

cout<<a[i][j]<<" ";

cout<<endl;}

cout<<"x=";cin>>x;

dfsuc(x);

cout<<endl<<"succesorii lui "<<x<<endl;

for(i=1;i<=n;i++)

if(suc[i]!=0)

cout<<i<<" ";

dfprec(x);

cout<<endl<<"Predecesorii lui "<<x<<endl;

for(i=1;i<=n;i++)

if(prec[i]!=0)

cout<<i<<" ";

cout<<endl<<"componenta tare conexa in care se gaseste "<<x<<" este "<<endl;

for(i=1;i<=n;i++)

if(prec[i]==suc[i]&&suc[i]!=0)

cout<<i<<" ";

getch();}