Notiunile cu care opereaza algoritmii

Algoritmii opereaza cu urmatoarele notiuni:

Un algoritm prelucreaza datele de intrare in scopul obtinerii unor rezultate (a datelor de iesire) utilizand si date intermediare.

Datele sunt valori concrete specifice fiecarei probleme care vor fi retinute de calculator in anumite zone de memorie.

Dimensiunea zonelor de memorie depinde de tipul datelor respective.

Intuitiv, memoria poate fi reprezentata ca locatii succesive (zone de memorie) identificate prin adrese (numere de ordine).

Programatorul are sarcina de a gandi algoritmul unei probleme si de a utiliza cat mai eficient memoria.

În program datele apar fie sub forma unor constante (valori cunoscute anticipat, care nu se modifica pe parcursul executiei), fie sub forma de variabile. Constantele si variabilele sunt obiectele informationale de baza manipulate într-un program.

Putem defini o variabila ca fiind un nume dat unei zone de memorie.

Datele se caracterizeaza printr-un anumit tip care va determina :

-o anumita multime din care data poate lua valori

- un anumit mod de reprezentare în memoria calculatorului

- o multime de operatori care pot fi aplicati acestor valori.

- tipul unei date determina lungimea zonei de memorie ocupata de acea data. În general, lungimea zonei de memorare este dependenta de calculatorul pe care s-a implementat compilatorul.

Datele se pot clasifica dupa tipul lor in:

¨ Caractere

¨ Intregi

¨ Reale

¨ Logice

¨ Sir de caractere

-variabilele: retin date de un tip anume. O variabila isi poate schimba valoarea dar tipul nu.

O variabila pentru a fi prelucrata trebuie sa fie declarata (anuntata). Acest lucru consta de fapt in precizarea tipului variabilei.

Exemplu:

caracter car

intreg a

real b,c

logic x

sir y

- expresii: o expresie este alcatuita din unul sau mai multi operanzi legati intre ei prin operatori. Operanzii pot fi constante sau variabile.

Exemplu:

4.5+2*a

unde 4.4, 2, a sunt operanzi iar + si * sunt operatori

Expresiile pot interveni cel mai adesea in instructiuni de atribuire de tipul:

variabila expresie

Exemplu:

c 2*b-1

Operatori pentru tipuri numerice :

operator	semnificatie
+	adunare
-	scadere
*	inmultire
/	catul impartirii
%	restul impartirii

Operatori relationali :

operator	semnificatie
=	De egalitate
<>	diferit
>	Mai mare
>=	Mai mare sau egal
<	Mai mic
<=	Mai mic sau egal

Operatori logici :

operator	semnificatie
!	Negatie logica
si	Si logic
sau	Sau logic

Datele de tip logic pot avea doua valori : A (adevarat) si F (fals)

Reguli de compunere a operatorilor logici :

!	A	F
	F	A

si	A	F
A	A	F
F	F	F

sau	A	F
A	A	A
F	A	F

Principiile programarii structurate

Programarea structurata a inceput la inceputul anilor 70. Este un concept cu o importanta fundamentala in scrierea algoritmilor.

In general, algoritmii se eleboreaza prin utilizarea exclusiva a anumitor structuri (liniara, alternativa, repetitiva).

Prin structura se intelege o anumita forma de imbinare a operatiilor cu care lucreaza algoritmii.

Structura liniara

Vom defini structura liniara astfel:

Daca S1, S2, S3,…Sn sunt structuri ( de orice tip), atunci:

S1

S2

S3

….

Sn

Constituie o strucura liniara reprezentata in pseudocod. Iar:

S2

….

Sn

Constituie o strucura liniara reprezentata in schema logica.

Structura alternativa

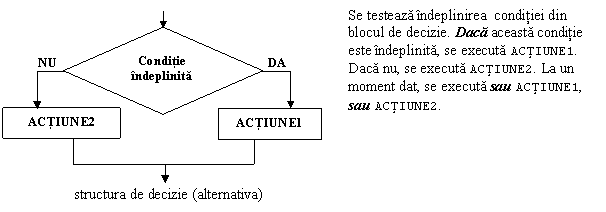
In pseudocod :

DACĂ condiţie=True

ATUNCI acţiune1

ALTFEL acţiune2

Exemple:

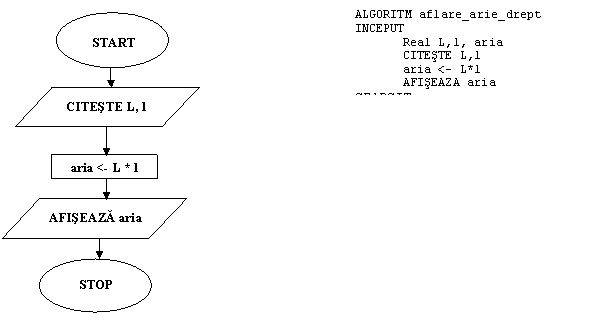
1. Se citesc 2 valori numerice reale, care reprezintă dimensiunile (lungimea şi lăţimea unui dreptunghi). Să se calculeze şi să se afişeze aria dreptunghiului.

Se citesc 2 valori reale. Să se afiseze valoarea maximului dintre cele 2 numere.

	ALGORITM max_2_nr ÎNCEPUT Real max, a, b CITEŞTE a, b DACA a >= b ATUNCI AFISEAZA a ALTFEL AFISEAZA b SFARŞIT

Structura repetitiva

Se evaluează condiţia de test (figura 1.5.). Dacă aceasta este îndeplinită, se execută ACŢIUNE. Se revine apoi şi se testează iar condiţia. Dacă este îndeplinită, se execută (se repetă) ACŢIUNE, ş.a.m.d. Abia în momentul în care condiţia nu mai este îndeplinită, se trece mai departe la urmatoarea operatie din algoritm. Astfel, cât timp condiţia este îndeplinită, se repetă ACŢIUNE. În cazul în care, la prima testare a condiţiei, aceasta nu este îndeplinită actiunea nu se executa nici macar odata.

Figura 1.5. Structură repetitivă cu test iniţial

Structuri repetitive cu test initial (fara contor)

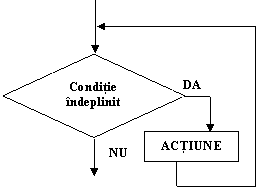
Observatie : actiune2 este de fapt actiunea care urmeaza structurii repetitive motiv pentru care in pseudocod se poate scrie :

CÂT TIMP condiţie

EXECUTĂ acţiune

Exisă şi situaţii în care se ştie de la început de câte ori se va repeta o anumită acţiune. În aceste cazuri se foloseşte tot o structură de control repetitivă cu test iniţial. Se utilizează un contor (numeric) pentru a ţine o evidenţă a numărului de execuţii ale acţiunii. De câte ori se execută acţiunea, contorul este incrementat.

Se atribuie contorului valoarea iniţială (figura 1.6.). Cât timp condiţia (valoarea contorului este mai mică sau egală cu valoarea finală) este îndeplinită, se repetă:

q ACŢIUNE

q incrementare contor (se adună 1 la valoarea anterioară a contorului).

In pseudocod :

PENTRU contor=val_ini LA val_finala [PAS p]

EXECUTĂ acţiune;

Structură repetitivă cu test final:

Structură repetitivă cu test final

In pseudocod :

REPETĂ

acţiune

PÂNĂ CÂND exp_test=TRUE