Arbore partial de
cost minim
Fie urmatoarea problema concreta:
Se dau n orase precum si costul conectarii anumitor
perechi de orase. Se cere sa se aleaga o parte din muchii astfel incat se
asigure existenta unui lant intre oricare doua orase si costul total sa fie
minim.
G=(V, E) un graf
neorientat, unde V are n elemente (n noduri) si E are m elemente (m muchii).
Se cunosc costurile muchiilor. Prin eliminarea unor muchii se obtine un
graf partial. Daca acesta este arbore se va numi arbore partial.
Costul unui arbore este egal cu suma costurilor muchiilor
sale. Arborele partial de cost minim este un arbore pentru care suma este
minima.
Problema. Fie un graf conex pentru care se cunosc
costurile muchiilor. Sa se determine arborele de cost minim asociat (costul
arborelui si vectorul de tati).
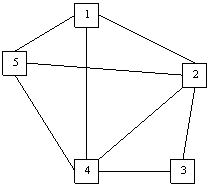
3
2
5
4 2 1 7
4
Vom utiliza 2
vectori :
- Vectorul s, pentru care s[i]=0 daca
nodul i a fost adaugat la arbore sau s[i]=k daca i nu a fost adaugat la
arbore si exista muchie intre i si k deja adaugat si are valoare minima
- Vectorul t, vector de tati
Algoritmul
consta in urmatoarele:
- Se citeste nodul de pornire , v
- Se incarca in s valoarea v
- S[v]=0 (arborele contine nodul
v)
Spre
exemplu daca v=1 se obtine:
S={0 1 1 1
1}
T={0 0 0 0
0}
- De n -1 ori :
- se determina cel mai apropiat nod (neadaugat inca la arbore) de
arborele partial construit si
muchia de cost minim min
- Se marcheaza pentru nod:
t[nod]=s[nod]
- Se adauga min la cost : cost=cost+min
- Se marcheaza nod ca fiind adaugat la
arbore: s[nod]=0
- Se actualizeaza datele :
§
Daca
distanta de la i la arbore (a[i][s[i]])
este mai mare decat distanta de la i la nodul nod tocmai adaugat la
arbore (a[i][nod]) se modifica potentialul ascendent pentru i: s[i]=nod
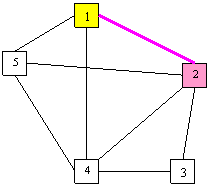
Pas1
Nod=2
Muchia de
cost minim este 1-2 min=2, cost=2
Se obtine :
S={0 0 2 2 1}
T={0 1 0 0 0}
3
2
5
4 2 1 7
4
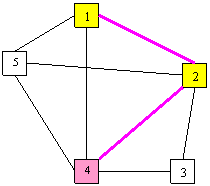
Pas2
Nod=4
Muchia de
cost minim este (2,4) min=1, cost=3
S={0 0 4 0 1}
T={0 1 0 2 0}
3 2
5
4 2 1 7
4
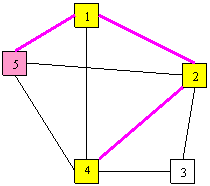
Pas 3
Nod=5
Muchia de
cost minim (1,5) min=3 cost=6
S={0,0,4,0,0}
T={0 1 0 2 1}
3
2
5
4 2 1 7
4
Pas 4
Nod=3
Muchia de
cost minim (4,3), min=4, cost=10
S={0 0 0 0 0}
T={0 1 4 2 1}
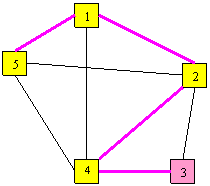
4
2
5
4 2 1 7
4
O solutie
de implementare:
#include<fstream.h>
#include<values.h>
#include<conio.h>
int
n,m,v,s[20],t[20];
long int
a[20][20],min;
const long
int infinit=MAXLONG;
void
citire()
{int
i,j,x,y,z;
fstream f;
f.open("arbminim.txt",ios::in);
if(f)
cout<<"ok"<<endl;
else cout<<"error!!";
f>>n>>m;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{if(i==j)
a[i][j]=0;
else
a[i][j]=infinit;
}
for(i=1;i<=m;i++)
{f>>x>>y>>z;
a[x][y]=a[y][x]=z;}
}
int cauta_nod(int
&nod)
{ min=infinit;
for(int i=1;i<=n;i++)
if(s[i]!=0)
if(a[i][s[i]]<min)
{min=a[i][s[i]];
nod=i;}
return min;
}
void
actualizeaza(int nod)
{for(int
i=1;i<=n;i++)
if(s[i])
if(a[i][s[i]]>a[i][nod])
s[i]=nod;
}
void main()
{ int
k,i,j,cost=0;
clrscr();
citire();
cout<<"nodul
de inceput ";
cin>>v;
s[v]=0;
for(i=1;i<=n;i++)
if(i!=v)
s[i]=v;
int nod;
for(k=1;k<=n-1;k++)
{min=cauta_nod(nod);
t[nod]=s[nod];
cost=cost+min;
s[nod]=0;
actualizeaza(nod);
}
cout<<"costul
este "<<cost<<endl;
cout<<"arborele
de cost minimal ";
for(i=1;i<=n;i++)
cout<<t[i]<<" ";
getch();
}
Probleme propuse
La construirea
unui nou oras intr cele n puncte comerciale sunt stabilite initial m drumuri de
acces intre perechi de puncte. Pentru fiecare dintre cele m perechi se cunoaste costul constructiei
drumului. Dupa o analiza a hartii s-a observat ca unele zone au ramas izolate
de altele si specialistii au ajuns la urmatoarea concluzie : sa se elimine
o parte din drumurile alese anterior dar sa se adauge drumuri noi de cost z
astfel incat sa se obtina o retea noua de drumuri pentru care costul total al
constructiei drumurilor sa fie minim si sa existe traseu de acces intre oricare
doua puncte comerciale . Sa se afiseze valoarea constructiei si un traseu
de la punctul comercial p la punctul 1.
Ex :
12
12
1 4 7
4 5 10
5 2 9
2 1 8
3 8 11
8 7 14
7 6 13
3 6 12
9 10 5
10 11 6
11 12 7
9 12 8
Z=100
Se afiseaza
costul 278
Traseul
de la 1 la 12 este :
1 8 12