Algoritmul
lui Roy-Floyd
Fie G=(V, E) un graf neorientat, unde V are n elemente
(n noduri) si E are m elemente (m
muchii) memorat prin matricea ponderilor. Se cere ca pentru doua noduri
x,y citite sa se determine lungimea minima a lantului de la x la y.
Astfel:
|
|
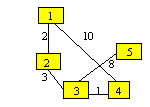
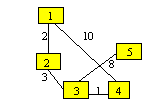
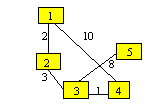
Initial matricea ponderilor pentru
nodurile 1 si 4 va retine 10. Se observa ca lantul
1,2,3,4 determina o suma a costurilor mai mica: 2+3+1=6. Lungime minima a lantului de la 1 la 4 este 6.
Algoritmul:
-se genereaza
matricea ponderilor:
|
|
0 2 pinf 10 pinf 2 0 3 pinf pinf pinf 3 0 1 8 10 pinf 1 0 pinf pinf pinf 8 pinf 0 |
Unde pinf
reprezinta plus infinit
-se incearca
pentru oricare pereche de noduri i,j sa se
obtina “drumuri” mai scurte prin noduri intermediare k (kÎ1…n).
Acest lucru se
determina comparand “lungimea” lantului a[i,j] cu lungimea lantului care trece
prin k si daca:
a[i,j] > a[i,k]+a[k,j] atunci se atribuie: a[i,j] ¬ a[i,k]+a[k,j]
Astfel generarea matricii drumurilor optime se realizeaza cu
urmatoarea secventa:
for(int
k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
Se obtine:
|
|
0 2 5 6 13 2 0 3 4 11 5 3 0 1 8 6 4 1 0 9 13 11 8 9 0 |
In
continuare, dupa determinarea matricii lanturilor optime, pentru doua noduri
citite x, y se cere sa se reconstituie un lant optim de la x la y (pot fi mai
multe solutii).
Solutie:
-se determina daca exista un lant de la x
la y (ar putea sa nu existe un astfel de lant daca graful nu este conex):
cand a[x,y] ¹¥
-se descompune “drumul” de la x la y prin k
atunci cand: a[x][y]=a[x][k]+a[k][y];
-
pentru
un astfel de algoritm se utilizeaza strategia Divide et Impera
Iata o
solutie:
#include<fstream.h>
#include<conio.h>
const
pinf=1000; //pentru
plus infinit
int
a[20][20],n,m;
void
citire_cost()
{fstream f;
int i,j,x,y,c;
f.open("roy.in",ios::in);
if(f)
cout<<"deschiderea a
reusit";
else
cout<<"eroare la
deschidere!";
cout<<endl;
f>>n>>m;
//initializare matrice
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
a[i][j]=0;
else
a[i][j]=pinf;
for(i=1;i<=m;i++)
{f>>x>>y>>c;
a[x][y]=a[y][x]=c;}
}
void
afisare_mat()
{for(int
i=1;i<=n;i++)
{for(int j=1;j<=n;j++)
if(a[i][j]==pinf)
cout<<"pinf ";
else
cout<<a[i][j]<<"
";
cout<<endl;}
}
void
genarare_matrice_drumuri_optime()
{for(int
k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[i][j]>a[i][k]+a[k][j])
a[i][j]=a[i][k]+a[k][j];
}
void
descompun_drum(int i,int j) //realizeaza
descompunerea portiunii de la i la j prin k
{int
g=0,k=1;
while(k<=n&&!g)
{if(i!=k&&j!=k)
if(a[i][j]==a[i][k]+a[k][j])
{descompun_drum(i,k);
descompun_drum(k,j);
g=1;} //g
marcheaza daca se poate realiza descompunerea
k++;
}
if(!g)
cout<<j<<" "; //cand
“drumul” nu mai poate fi descompus afisez extremitatea finala
}
void
scriu_drum(int nodini,int nodfin) // functia
primeste ca parametri cele doua noduri pt care se determina optimul
{if(a[nodini][nodfin]<pinf)
{cout<<"lantul de la "<<nodini<<" la
"<<nodfin<<" are lungimea "<<a[nodini][nodfin];
cout<<endl<<"un drum
optim este: "<<endl;
cout<<nodini<<" ";
descompun_drum(nodini,nodfin); // apeleaza functia care afiseaza efectiv lantul
}
else
cout<<"nu exista drum de la
"<<nodini<<" la "<<nodfin;
}
void main()
{clrscr();int
x,y;
citire_cost();
cout<<endl<<"matricea
ponderilor "<<endl;
afisare_mat();
genarare_matrice_drumuri_optime();
cout<<endl<<"matricea
drumurilor optime "<<endl;
afisare_mat();
cout<<endl<<"Se
determina drumul minim intre varfurile x si y "<<endl;
cout<<"x=";
cin>>x;
cout<<"y=";
cin>>y;
scriu_drum(x,y);
getch();
}
Probleme
propuse:
▪
Intre
n statii spatiale se stabilesc trasee. Se cunosc traseele directe intre perechi
de statii si distanta dintre ele. Sa se determine drumul minim intre doua
statii date stiind ca nu pot fi doua statii pare una dupa cealalta. Sa se afiseze drumul de la statia x la
statia y.
▪
Reteaua
de strazi a unui oras este reprezentata prin nodurile intersectii ale orasului.
Din intersectiile A si B pleaca doi pietoni spre intersectiile x, respectiv y.
Ei conosc bine orasul si merg spre destinatie pe drumul minim. Stabiliti daca
traseele au trecut prin puncte comune si care sunt aceste intersectii.
Determinati daca exista intersectiile in care s-au intalnit.
▪
Intr-o tabara, elevii au n puncte de plecare (cantina, corturile,
stejarul cel batran etc.). Initial,
deplasarea intre oricare doua puncte se face intr-un timp t, insa organizatorii
au amplasat m obstacole pe traseele dintre aceste puncte. Cu fiecare obstacol
care trebuie depasit, elevii pierd 30 de secunde. Pe
un traseu pot fi mai multe obstacole. Elevii vor sa ajunga
din punctul X in punctul Y, pe drumul cel mai scurt. Scrieti
un program care citeste n, X, Y. Apoi m perechi de
puncte intre care sunt amplasate obstacole si afiseaza
drumul cel mai rapid intre X si Y.