SIMULAREA EXAMENULUI DE BACALAUREAT

Teza la informatica- Semestrul II- clasa a XI-a Varianta B

1.	Fie matricea de adiacente a unui graf neorientat: 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0 Stabiliti daca graful este:
a.	conex			b.	hamiltonian
c.	ciclic			d.	eulerian
2.	Considerând un graf neorientat având nodurile notate cu 1, 2, 3, 4, 5, corespunzător liniilor matricei de adiacenţă date, stabiliţi dacă nodurile 1 şi 3:			0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0
a.	sunt noduri izolate			b.	aparţin aceleiaşi componente conexe
c.	sunt conectate printr-un lanţ			d.	sunt noduri adiacente
3.	Se consideră un graf neorientat cu 7 noduri şi 3 muchii. Graful:
a.	Nu poate fi conex	b.	Nu poate contine cicluri	c.	Poate fi arbore		d.	Este graf hamiltonian
4.	Se consideră un graf orientat cu 6 noduri etichetate cu numere de la 1 la 6 şi 6 arce astfel încât există un arc de la fiecare nod cu eticheta i către un nod cu eticheta i*2 dacă există un astfel de nod sau către nodul cu eticheta i –1 în caz contrar.
a.	Graful este complet			b.	Graful este tare conex
c.	Graful nu contine circuite			d.	Graful este arborescenta
5.	Considerând un graf orientat având matricea de adiacenţă alturată, stabiliţi câte dintre nodurile grafului nu au gradul interior (intern) egal cu gradul exterior (extern):					0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0
a.	3			b.	4
c.	2			d.	5
6.	Se consideră un arbore cu următoarele proprietăţi: rădăcina este nodul 1 (considerat de nivel 1) şi fiecare nod i (cu 1£ i £ 3) aflat pe nivelul j are ca descendenţi nodurile i+j şi i+2*j. Nodurile i cu (cu i > 3) sunt noduri terminale (frunze).
a.	Nu se poate construi un astfel de arbore			b.	Are 5 frunze
c.	Are 2 nivele			d.	Arborele este binar
7.	Orice graf neorientat cu n noduri are o matrice de adiacenţă cu următoarea proprietate:
a.	are suma elementelor egală cu n			b.	este simetrică faţă de diagonala secundară
c.	este simetrică faţă de diagonala principală			d.	este formată numai din valorile 0, 1 şi –1
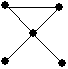
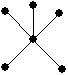
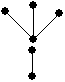
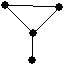
8.	Stabiliţi care dintre grafurile următoare este un arbore:
a.		b.		c.			d.
9.	Care este matricea de adiacenţă a unui graf neorientat cu 4 noduri, 2 muchii şi cel puţin un nod izolat?
a.	0 0 1 0 0 1 1 1 0	b.	0 1 1 0 1 0 0 0 1 0 1 0 0 0 0 0	c.	0 1 0 1 1 0 0 0 0 0 0 0 1 0 0 0		d.	0 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0

10. Fie arborele binar din figura urmatoare:

a)Care este sirul de date de intrare necesar generarii grafului?

b) Parcurgeti arborele prin cele 3 metode specifice arborilor binari

11. Intr-un fisier sunt memorate n numere naturale. Intre cele n numere se stabileste o relatie de tip arbore oarecare. In fisier sunt scrie pe prima linie n, pe linia a doua cele n valori iar pe linia a treia vectorul de tip tata asociat.

a) Sa se afiseze valorile asociate nodurilor terminale

b) Sa se afiseze valoarea asociata radacinii

c) Sa se se afiseze numerele care contin o cifra citita de la tastatura asociate arborelui pe linie ascendenta incepand de la un nod pana la radacina.Numarul de ordine al nodului de pornire se citeste de la tastatura.

Exemplu:

12 14 13 25 43 82 21 cele 7 numere

0 1 1 3 3 1 5

se citeste nodul 7 si cifra 3

Se afiseaza 43 13

Barem de corectare:

Oficiu

total

0.5

0.75

1.5